题目内容
在△ABC中,AB=AC,D为△ABC外一点,且∠BAC+∠BDC=180°,探索∠BDA与∠CDA的数量关系,并证明你的结论.
考点:全等三角形的判定与性质
专题:
分析:延长DC到E,使CE=BD,连结AE,易证∠ACE=∠ABD,即可证明△ACE≌△ABD,即可求得AD=AE,∠ADB=∠E,即可解题.
解答:解:结论为∠ADC=∠ADB,
理由如下:延长DC到E,使CE=BD,连结AE,

∵∠BAC+∠BDC=180°,四边形内角和为360°,
∴∠ABD+∠ACD=180°,
∵∠ACD+∠ACE=180°,
∴∠ACE=∠ABD,
在△ACE和△ABD中,
,
∴△ACE≌△ABD,(SAS)
∴AD=AE,∠ADB=∠E,
∴∠ADC=∠E=∠ADB.
理由如下:延长DC到E,使CE=BD,连结AE,

∵∠BAC+∠BDC=180°,四边形内角和为360°,
∴∠ABD+∠ACD=180°,
∵∠ACD+∠ACE=180°,
∴∠ACE=∠ABD,
在△ACE和△ABD中,
|
∴△ACE≌△ABD,(SAS)
∴AD=AE,∠ADB=∠E,
∴∠ADC=∠E=∠ADB.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ACE≌△ABD是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知4x=5y,则y:x的值为( )
| A、1:5 | B、5:1 |
| C、4:5 | D、5:4 |
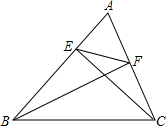 如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,
如图,已知△ABC中CE⊥AB于E,BF⊥AC于F, 如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.当AD=2时,则AE的长为
如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.当AD=2时,则AE的长为 如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.求证:PB+PC=PA.
如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.求证:PB+PC=PA. 如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为
如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为