题目内容
 如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.求证:PB+PC=PA.
如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.求证:PB+PC=PA.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:过点A作AM⊥BP,AN⊥PN,交PC的延长线于点N,可得∠AMB=∠ANC=90°,在AP上截取PE,使得PE=PB,连接BE,易证△ABM≌△ACN,可得AM=AN,即可求得∠APB=60°,进而可以求证△ABE≌△CBP,可得AE=CP,即可解题.
解答:证明:过点A作AM⊥BP,AN⊥PN,交PC的延长线于点N,可得∠AMB=∠ANC=90°,在AP上截取PE,使得PE=PB,连接BE,

∵∠ACN+∠ACP=180°,且∠ABM+∠ACP=180°,
∴∠ACN=∠ABM,
又△ABC是等边三角形,
∴AB=AC,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(AAS),
∴AM=AN,又AM⊥BP,AN⊥PN,
∴∠APB=∠APC,
∵∠ABP+∠ACP=180°,
∴∠BAC+∠BPC=180°,
∴∠BPC=120°,
∴∠APB=∠APC=60°,
∵PB=PE,
∴△PEB是等边三角形
∴PB=BE,∠EBP=60°,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∴∠EBP=∠ABC,
∴∠ABE=∠PBC,
在△ABE和△CBP中,
,
∴△ABE≌△CBP,(SAS)
∴AE=CP,
∵AP=AE+PE,
∴AP=PB+PC.

∵∠ACN+∠ACP=180°,且∠ABM+∠ACP=180°,
∴∠ACN=∠ABM,
又△ABC是等边三角形,
∴AB=AC,
在△ABM和△ACN中,
|
∴△ABM≌△ACN(AAS),
∴AM=AN,又AM⊥BP,AN⊥PN,
∴∠APB=∠APC,
∵∠ABP+∠ACP=180°,
∴∠BAC+∠BPC=180°,
∴∠BPC=120°,
∴∠APB=∠APC=60°,
∵PB=PE,
∴△PEB是等边三角形
∴PB=BE,∠EBP=60°,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∴∠EBP=∠ABC,
∴∠ABE=∠PBC,
在△ABE和△CBP中,
|
∴△ABE≌△CBP,(SAS)
∴AE=CP,
∵AP=AE+PE,
∴AP=PB+PC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABM≌△ACN和△ABE≌△CBP是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下列计算错误的是( )
| A、1010÷a9=a |
| B、b6÷b4=b2 |
| C、a5÷a2=a3 |
| D、(-bx)4÷(-bx)2=-b2x2 |
计算
-
的结果是( )
| x2 |
| x-1 |
| x |
| x-1 |
| A、x |
| B、1 |
| C、-x2+x |
| D、x-1 |
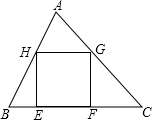 如下图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15,BC边上的高是10,则正方形的面积为( )
如下图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15,BC边上的高是10,则正方形的面积为( )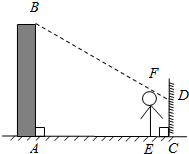 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,