题目内容
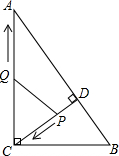 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
考点:相似形综合题,一元二次方程的应用,等腰三角形的性质,勾股定理,相似三角形的判定与性质
专题:压轴题
分析:(1)利用勾股定理可求出AB长,再用等积法就可求出线段CD的长.
(2)过点P作PH⊥AC,垂足为H,通过三角形相似即可用t的代数式表示PH,从而可以求出S与t之间的函数关系式;利用S△CPQ:S△ABC=9:100建立t的方程,解方程即可解决问题.
(3)可分三种情况进行讨论:由CQ=CP可建立关于t的方程,从而求出t;由PQ=PC或QC=QP不能直接得到关于t的方程,可借助于等腰三角形的三线合一及三角形相似,即可建立关于t的方程,从而求出t.
(2)过点P作PH⊥AC,垂足为H,通过三角形相似即可用t的代数式表示PH,从而可以求出S与t之间的函数关系式;利用S△CPQ:S△ABC=9:100建立t的方程,解方程即可解决问题.
(3)可分三种情况进行讨论:由CQ=CP可建立关于t的方程,从而求出t;由PQ=PC或QC=QP不能直接得到关于t的方程,可借助于等腰三角形的三线合一及三角形相似,即可建立关于t的方程,从而求出t.
解答: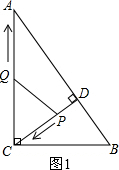 解:(1)如图1,
解:(1)如图1,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵CD⊥AB,
∴S△ABC=
BC?AC=
AB?CD.
∴CD=
=
=4.8.
∴线段CD的长为4.8.
(2)①过点P作PH⊥AC,垂足为H,如图2所示.
由题可知DP=t,CQ=t.
则CP=4.8-t.
∵∠ACB=∠CDB=90°,
∴∠HCP=90°-∠DCB=∠B.
∵PH⊥AC,
∴∠CHP=90°.
∴∠CHP=∠ACB.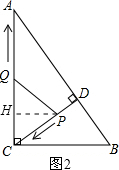
∴△CHP∽△BCA.
∴
=
.
∴
=
.
∴PH=
-
t.
∴S△CPQ=
CQ?PH=
t(
-
t)=-
t2+
t.
②存在某一时刻t,使得S△CPQ:S△ABC=9:100.
∵S△ABC=
×6×8=24,
且S△CPQ:S△ABC=9:100,
∴(-
t2+
t):24=9:100.
整理得:5t2-24t+27=0.
即(5t-9)(t-3)=0.
解得:t=
或t=3.
∵0≤t≤4.8,
∴当t=
秒或t=3秒时,S△CPQ:S△ABC=9:100.
(3)①若CQ=CP,如图1,
则t=4.8-t.
解得:t=2.4.
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH=
QC=
.
∵△CHP∽△BCA.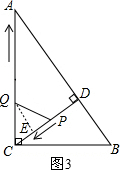
∴
=
.
∴
=
.
解得:t=
.
③若QC=QP,
过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得:t=
.
综上所述:当t为2.4秒或
秒或
秒时,△CPQ为等腰三角形.
 解:(1)如图1,
解:(1)如图1,∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵CD⊥AB,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| BC?AC |
| AB |
| 6×8 |
| 10 |
∴线段CD的长为4.8.
(2)①过点P作PH⊥AC,垂足为H,如图2所示.
由题可知DP=t,CQ=t.
则CP=4.8-t.
∵∠ACB=∠CDB=90°,
∴∠HCP=90°-∠DCB=∠B.
∵PH⊥AC,
∴∠CHP=90°.
∴∠CHP=∠ACB.

∴△CHP∽△BCA.
∴
| PH |
| AC |
| PC |
| AB |
∴
| PH |
| 8 |
| 4.8-t |
| 10 |
∴PH=
| 96 |
| 25 |
| 4 |
| 5 |
∴S△CPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 96 |
| 25 |
| 4 |
| 5 |
| 2 |
| 5 |
| 48 |
| 25 |
②存在某一时刻t,使得S△CPQ:S△ABC=9:100.
∵S△ABC=
| 1 |
| 2 |
且S△CPQ:S△ABC=9:100,
∴(-
| 2 |
| 5 |
| 48 |
| 25 |
整理得:5t2-24t+27=0.
即(5t-9)(t-3)=0.
解得:t=
| 9 |
| 5 |
∵0≤t≤4.8,
∴当t=
| 9 |
| 5 |
(3)①若CQ=CP,如图1,
则t=4.8-t.
解得:t=2.4.
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH=
| 1 |
| 2 |
| t |
| 2 |
∵△CHP∽△BCA.

∴
| CH |
| BC |
| CP |
| AB |
∴
| ||
| 6 |
| 4.8-t |
| 10 |
解得:t=
| 144 |
| 55 |
③若QC=QP,
过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得:t=
| 24 |
| 11 |
综上所述:当t为2.4秒或
| 144 |
| 55 |
| 24 |
| 11 |
点评:本题考查了相似三角形的判定与性质、等腰三角形的性质、一元二次方程的应用、勾股定理等知识,具有一定的综合性,而利用等腰三角形的三线合一巧妙地将两腰相等转化为底边上的两条线段相等是解决第三小题的关键.
相关练习册答案:

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知m,n是方程x2-x-1=0的两实数根,则
+
的值为( )
| 1 |
| m |
| 1 |
| n |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
下列计算正确的是( )
| A、a3+a3=2a6 |
| B、a3•a2=a6 |
| C、a6÷a2=a3 |
| D、(a3)2=a6 |
 如图,BE⊥AE,CF⊥AE,垂足分别是E、F,又知D是EF的中点,△BED与△CFD全等吗?为什么?
如图,BE⊥AE,CF⊥AE,垂足分别是E、F,又知D是EF的中点,△BED与△CFD全等吗?为什么? 在Rt△ABC中,∠C=90°,∠B=60°,BC=5cm,求AC的长.
在Rt△ABC中,∠C=90°,∠B=60°,BC=5cm,求AC的长. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.