题目内容
 如图,BE⊥AE,CF⊥AE,垂足分别是E、F,又知D是EF的中点,△BED与△CFD全等吗?为什么?
如图,BE⊥AE,CF⊥AE,垂足分别是E、F,又知D是EF的中点,△BED与△CFD全等吗?为什么?考点:全等三角形的判定
专题:
分析:根据角边角公里可得出△BED与△CFD全等.由BE⊥AE,CF⊥AE,得∠BED=∠CFD,再由D是EF的中点,得ED=FD,从而得出△BED与△CFD全等.
解答:解:△BED≌△CFD.
理由是:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA).
理由是:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
|
∴△BED≌△CFD(ASA).
点评:本题考查了全等三角形的判定,判定一般三角形全等有SSS、SAS、ASA、AAS,判定两个直角三角形全等还有HL.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )A、(
| ||||
| B、(3,3) | ||||
C、(
| ||||
D、(
|
 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x秒后两车间的距离为y米,关于y关于x的函数关系如图所示,则甲车的速度是( )米/秒.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x秒后两车间的距离为y米,关于y关于x的函数关系如图所示,则甲车的速度是( )米/秒.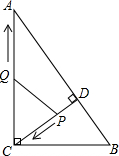 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒. 如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.