题目内容
2. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1.(1)求BD的长;
(2)求△ACD与△ABD的面积比.
分析 (1)根据角平分线的性质得到DC=DE=1,根据直角三角形的性质求出答案;
(2)根据高相等的两个三角形的面积比等于底的比计算即可.
解答 解:(1)∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE=1,
∵DE⊥AB,∠B=30°,CD=1,
∴BD=2DE=2;
(2)△ACD与△ABD的面积比=CD:BD=1:2.
点评 本题考查的是角平分线的性质和直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键,注意在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
14.△ABC中,已知AB=AC,∠BAC=120°,DE垂直平分AB,交BC于D,垂足为E,且DE=4cm,则BC长为( )
| A. | 15cm | B. | 16cm | C. | 20cm | D. | 24cm |
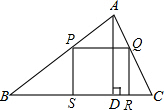 一块铁皮呈锐角三角形,它的一边BC=80cm,高AD=60cm.要把它加工成矩形零件PQRS,使矩形的一边SR位于边BC上,另两个顶点P、Q分别在边AB、AC上,请你设计一个加工方案,使矩形零件的面积最大,并求出最大面积.
一块铁皮呈锐角三角形,它的一边BC=80cm,高AD=60cm.要把它加工成矩形零件PQRS,使矩形的一边SR位于边BC上,另两个顶点P、Q分别在边AB、AC上,请你设计一个加工方案,使矩形零件的面积最大,并求出最大面积.