题目内容
2.若一次函数y=(m+1)x+3-m的图象经过一、二、三象限,则m的取值范围是-1<m<3.分析 图象经过一、三象限,则2m+4>0;图象还过第二象限,所以直线与y轴的交点在正半轴上,则3-m>0.综合求解.
解答 解:∵图象经过一、三象限,则m+1>0,解得m>-1;
图象还过第二象限,所以直线与y轴的交点在正半轴上,则3-m>0,解得m<3.
∴m的取值范围是-1<m<3.
故答案为:-1<m<3.
点评 此题考查了一次函数的图象与系数的关系,一次函数的图象经过第几象限,取决于x的系数及常数是大于0或是小于0.可借助草图分析.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
12.把抛物线y=$\frac{1}{2}$(x-2)2-3绕顶点旋转180°,得到的抛物线的表达式是y=-$\frac{1}{2}$(x-2)2-3,再将其向上平移3个单位,抛物线的顶点落在x轴上.
10.对于一个一次函数,x每增加1,y的值就减少2,且它的图象经过(0,3)点,则该函数的表达式为( )
| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
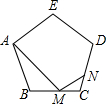 如图,点M为正五边形ABCDE的边BC上一点,$\frac{BM}{CM}$=2,连结AM,作∠AMN=108°,MN交CD于点N,则$\frac{CN}{ND}$的值为$\frac{2}{7}$.
如图,点M为正五边形ABCDE的边BC上一点,$\frac{BM}{CM}$=2,连结AM,作∠AMN=108°,MN交CD于点N,则$\frac{CN}{ND}$的值为$\frac{2}{7}$.