题目内容
已知：如图，△ABC中，∠ACB=90°，CD⊥AB于D，AB=10，BC=6．求：sin∠ACD的值及AD的长．考点：解直角三角形
专题：
分析：根据勾股定理可以求得AC的长度，即可求得sin∠ACD的值，再根据AC的长即可求得AD的长．
解答：解：∵CD⊥AB，∠ACB=90°，
∴∠B=∠ACD，
RT△ABC中，AC=
=8，
∴sin∠ACD=sinB=
=
，
∴AD=AC•sin∠ACD=
．
∴∠B=∠ACD，
RT△ABC中，AC=
| AB2-BC2 |
∴sin∠ACD=sinB=
| AC |
| AB |
| 4 |
| 5 |
∴AD=AC•sin∠ACD=
| 32 |
| 5 |
点评：本题考查了直角三角形中正弦值的计算，考查了勾股定理的运用，本题中求AC的长是解题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
已知CA、BE分别垂直AB于A点和B点，∠CDE=90°，
如图，Rt△ABC中，∠BAC=90°，∠ACB=30°，点A的坐标为（3，0），过点B的双曲线y=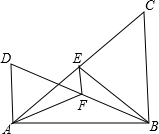
如图，∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点．
如图，矩形ABCD的面积为1，它的两条对角线交于点O1，取BO1的中点O2，连AO2并延长到C1，使得AO2=C1O2，得到四边形ABC1O1，同样取BO2的中点O3，连AO3并延长到C2，使得AO3=C2O3，得到四边形ABC2O2…依此类推，可作得四边形ABCnOn．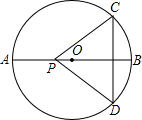
如图，已知：⊙O中AB是直径，点P在AB上，PB平分∠CPD，求证：PC=PD．
如图，△ABC中，∠C=90°，∠A=30°，已知AC=3，求周长．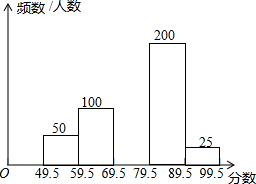
某市为了解参加历史科结业的2万名学生的考试成绩情况，现从中随机抽取部分学生的成绩作为一个样本，整理后分成5组，绘制了频数分布直方图，其中，第二组的频率为0.2．