题目内容
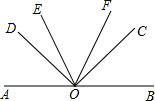 如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;
如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;(1)若∠BOC=40°,求∠EOF的度数;
(2)当OD平分∠AOF时,求∠BOC的度数.
考点:角的计算,角平分线的定义
专题:
分析:(1)由∠BOC=40°,∠COD=90°,可求得∠AOD,∠AOC与∠BOD的度数,又由OE平分∠AOC,OF平分∠BOD,即可求得∠AOE与∠BOF的度数,继而求得∠EOF的度数;
(2)由O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD,可用∠BOC表示出各角,然后由OD平分∠AOF时,得到:2(90°-∠BOC)=135°-
∠BOC,继而求得答案.
(2)由O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD,可用∠BOC表示出各角,然后由OD平分∠AOF时,得到:2(90°-∠BOC)=135°-
| 1 |
| 2 |
解答:解:(1)∵∠BOC=40°,∠COD=90°,
∴∠AOD=180°-∠COD-∠BOC=50°,
∴∠AOC=∠AOD+∠COD=140°,∠BOD=∠COD+∠BOC=130°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=
∠AOC=70°,∠BOF=
∠BOD=65°,
∴∠EOF=180°-∠AOE-∠BOF=45°;
(2)∵∠COD=90°,
∴∠AOD=180°-∠COD-∠BOC=90°-∠BOC,
∴∠AOC=∠AOD+∠COD=180°-∠BOC,∠BOD=∠COD+∠BOC=90°+∠BOC,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=
∠AOC=90°-
∠BOC,∠BOF=
∠BOD=45°+
∠BOC,
∴∠EOF=180°-∠AOE-∠BOF=45°;
∴∠AOF=∠AOE+∠EOF=135°-
∠BOC,
∵OD平分∠AOF,
∴∠AOF=2∠AOD,
∴2(90°-∠BOC)=135°-
∠BOC,
解得:∠BOC=30°.
∴∠AOD=180°-∠COD-∠BOC=50°,
∴∠AOC=∠AOD+∠COD=140°,∠BOD=∠COD+∠BOC=130°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=180°-∠AOE-∠BOF=45°;
(2)∵∠COD=90°,
∴∠AOD=180°-∠COD-∠BOC=90°-∠BOC,
∴∠AOC=∠AOD+∠COD=180°-∠BOC,∠BOD=∠COD+∠BOC=90°+∠BOC,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=180°-∠AOE-∠BOF=45°;
∴∠AOF=∠AOE+∠EOF=135°-
| 1 |
| 2 |
∵OD平分∠AOF,
∴∠AOF=2∠AOD,
∴2(90°-∠BOC)=135°-
| 1 |
| 2 |
解得:∠BOC=30°.
点评:此题考查了角的计算与角平分线的定义.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式能运用平方差公式分解因式的有( )
①x2-2xy+y2 ②-4x2+y2 ③-4x2-y2 ④(x-y)3-y+x.
①x2-2xy+y2 ②-4x2+y2 ③-4x2-y2 ④(x-y)3-y+x.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°.
如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°.