题目内容
 如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°.
如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°.(1)求∠B,∠C和∠BAD的度数.
(2)当AC=8m时,求AD的长.
考点:等腰三角形的性质,含30度角的直角三角形
专题:
分析:(1)等腰三角形的三线合一的性质即可求解;
(2)含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.依此即可求解.
(2)含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.依此即可求解.
解答:解:(1)∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120°.
∠B=∠C=(180°-120°)÷2=30°,
∠BAD=
∠BAC=60°;
(2)∵在△ABC中,AC=8m,∠C=30°,
∴AD=
AC=4m.
∠B=∠C=(180°-120°)÷2=30°,
∠BAD=
| 1 |
| 2 |
(2)∵在△ABC中,AC=8m,∠C=30°,
∴AD=
| 1 |
| 2 |
点评:本题考查含30度角的直角三角形,等腰三角形的性质,三线合一,高线,中线,角平分线重合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
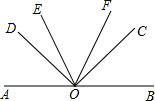 如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;
如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;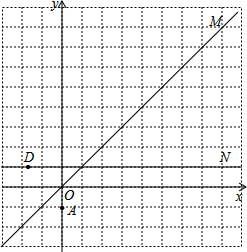 如图,在平面直角坐标系中O为坐标原点,直线OM是一、三象限的角平分线,直线DN是过点(0,1)与x轴平行的直线,一颗棋子从点A(0,-1)处开始依次关于直线OM、直线DN作循环对称变换,即第一次跳到点A关于直线OM的对称点A1处,接着跳到点A1关于直线DN的对称点A2处,第三次再跳到点A2关于直线OM的对称点A3处,….如此下去.
如图,在平面直角坐标系中O为坐标原点,直线OM是一、三象限的角平分线,直线DN是过点(0,1)与x轴平行的直线,一颗棋子从点A(0,-1)处开始依次关于直线OM、直线DN作循环对称变换,即第一次跳到点A关于直线OM的对称点A1处,接着跳到点A1关于直线DN的对称点A2处,第三次再跳到点A2关于直线OM的对称点A3处,….如此下去.