题目内容
3.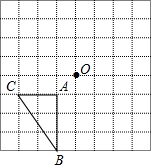 如图所示,△ABC的顶点与点O在8×8的网格中的格点上.
如图所示,△ABC的顶点与点O在8×8的网格中的格点上.(1)画出△ABC绕点O顺时针旋转90°得到的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°得到的△A2B2C2;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为$\frac{\sqrt{13}}{2}$.
分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)直接利用旋转的性质得出对应点位置进而得出答案;
(3)利用直角三角形的性质得出其斜边长为外接圆直径,进而得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)⊙M能盖住△ABC,则⊙M的半径最小值时,其直径为BC,
故⊙M的半径最小值为:$\frac{\sqrt{13}}{2}$.
故答案为:$\frac{\sqrt{13}}{2}$.
点评 此题主要考查了旋转变换以及直角三角形的性质,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
14.若分式$\frac{2x+2}{3x-6}$无意义,那么x的取值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
18.若一个60°的角绕顶点旋转15°,则旋转前后重叠部分角的大小是( )
| A. | 15° | B. | 45° | C. | 60° | D. | 75° |
8.声音在空气中传播每小时约通过1200000m,将1200000用科学记数法表示为( )
| A. | 12×106 | B. | 1.2×106 | C. | 1.2×107 | D. | 1.2×108 |
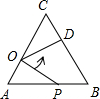 如图,在等边△ABC中,AC=9,AO=3,点P是AB上一动点,OP=OD,∠POD=60°,则AP=6.
如图,在等边△ABC中,AC=9,AO=3,点P是AB上一动点,OP=OD,∠POD=60°,则AP=6. 如图,已知∠B=30°,∠D=20°,∠BCD=50°,那么AB∥DE吗?请说明理由.
如图,已知∠B=30°,∠D=20°,∠BCD=50°,那么AB∥DE吗?请说明理由.