题目内容
12.对x,y定义了一种新运算T,规定T(x,y)=$\frac{ax+by}{2x+y}$(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=$\frac{a×0+b×1}{2×0+1}$,已知T(1,-1)=-2,T(4,2)=1.(1)求a,b的值;
(2)若关于m的不等式组$\left\{\begin{array}{l}{T(2m,5-4m)≤4}\\{T(m,3-2m)>p}\end{array}\right.$恰好有3个整数解,求p的取值范围.
分析 (1)根据题中的新定义列出关于a与b的方程组,求出方程组的解即可得到a与b的值;
(2)利用题中的新定义化简已知不等式组,表示出解集,由不等式组恰好有3个整数解,确定出p的范围即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a-b=-2①}\\{2a+b=5②}\end{array}\right.$,
①+②得:3a=3,即a=1,
把a=1代入①得:b=3;
(2)根据题意得:$\left\{\begin{array}{l}{\frac{2m+3(5-4m)}{4m+5-4m}≤4①}\\{\frac{m+3(3-2m)}{2m+3-2m}>p②}\end{array}\right.$,
由①得:m≥-$\frac{1}{2}$;由②得:m<$\frac{9-3p}{5}$,
∴不等式组的解集为-$\frac{1}{2}$≤m<$\frac{9-3p}{5}$,
∵不等式组恰好有3个整数解,集m=0,1,2,
∴2<$\frac{9-3p}{5}$≤3,
解得:-2≤p<-$\frac{1}{3}$.
点评 此题考查了解二元一次方程组,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若x>y,则下列式子中错误的是( )
| A. | x-3>y-3 | B. | x+3>y+3 | C. | $\frac{1}{3}x>\frac{1}{3}y$ | D. | -3x>-3y |
17.要使(x+m)(x-3)的结果中不含x的一次项,则m等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
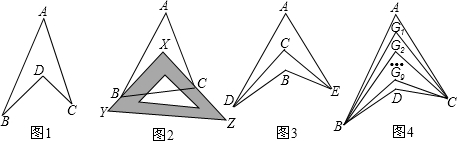
 如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.
如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.