题目内容
8.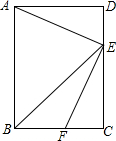 如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.
如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.(1)如果FE⊥AE,那么FE和AE相等吗?证明你的结论.
(2)如果FE=AE,那么FE与AE有怎样的位置关系?证明你的结论.
分析 (1)根据角平分线的定义可得∠ABE=∠CBE,根据两直线平行,内错角相等可得∠ABE=∠BEC,然后求出∠CBE=∠BEC,根据等角对等边可得BC=CE,根据矩形的对边相等可得AD=BC,从而得到AD=CE,再根据同角的余角相等求出∠DAE=∠CEF,然后利用“角边角”证明△ADE和△ECF全等,根据全等三角形对应边相等可得FE=AE;
(2)同(1)求出AD=CE,然后利用“HL”证明Rt△ADE和Rt△ECF全等,根据全等三角形对应角相等可得∠DAE=∠CEF,然后求出∠AED+∠CEF=90°,再根据平角等于180°求出∠AEF=90°,然后根据垂直的定义证明即可.
解答 证明:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵矩形对边AB∥CD,
∴∠ABE=∠BEC,
∴∠CBE=∠BEC,
∴BC=CE,
∵矩形ABCD的对边AD=BC,
∴AD=CE,
∵FE⊥AE,
∴∠AED+∠CEF=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠CEF,
在△ADE和△ECF中,
$\left\{\begin{array}{l}{∠DAE=∠CEF}\\{AD=CE}\\{∠C=∠D=90°}\end{array}\right.$,
∴△ADE≌△ECF(ASA),
∴FE=AE;
(2)同(1)可证AD=CE,
在Rt△ADE和Rt△ECF中,
$\left\{\begin{array}{l}{FE=AE}\\{AD=CE}\end{array}\right.$,
∴Rt△ADE≌Rt△ECF(HL),
∴∠DAE=∠CEF,
∴∠AED+∠CEF=∠AED+∠DAE=90°,
∴∠AEF=180°-(∠AED+∠CEF)=180°-90°=90°,
∴FE⊥AE.
点评 本题考查了全等三角形的判定与性质,矩形的性质,角平分线的定义,平行线的性质,熟记各性质并准确识图确定出全等三角形是解题的关键.

 习题精选系列答案
习题精选系列答案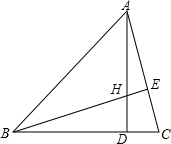 如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=45°.
如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=45°.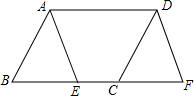 如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.
如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.