题目内容
对于二次函数y=
x2,点(0,
)叫作该函数图象的焦点.例如y=
x2的图象的焦点坐标为(0,1),y=x2+2x+3的图象的焦点坐标是 .
| 1 |
| 2p |
| p |
| 2 |
| 1 |
| 4 |
考点:二次函数图象上点的坐标特征
专题:新定义
分析:先把y=x2+2x+3配成顶点式得到顶点坐标为(-1,2),再利用抛物线的平移,把抛物线y=(x+1)2+2先向右平移1个单位,再向下平移2个单位得到抛物线y=x2,根据新定义易得抛物线y=x2的焦点坐标为(0,
),然后把点(0,
)反向平移即可得到答案.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:y=x2+2x+3=(x+1)2+2,抛物线y=x2+2x+3的顶点坐标为(-1,2),把抛物线y=(x+1)2+2先向右平移1个单位,再向下平移2个单位得到抛物线y=x2,而抛物线y=x2的焦点坐标为(0,
),
由于点(0,
)向左平移1个单位,再向上平移2个单位得到对应点的坐标为(-1,
),所以y=x2+2x+3的图象的焦点坐标是(-1,
).
故答案为(-1,
).
| 1 |
| 4 |
由于点(0,
| 1 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
故答案为(-1,
| 9 |
| 4 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了理解能力.

练习册系列答案
相关题目
关于x的一元二次方程(m-3)x2+(3m-1)x+m2-9=0的一个根是0,则m的值是( )
| A、3 | B、-3 | C、3或-3 | D、0 |
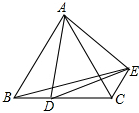 如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )
如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )A、2
| ||
B、
| ||
C、4
| ||
| D、7 |
 已知:如图,直线EF与AB,CD分别交于点G,H,∠1=∠2,∠D=50°,求∠B的度数.
已知:如图,直线EF与AB,CD分别交于点G,H,∠1=∠2,∠D=50°,求∠B的度数. 用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图,想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块?
用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图,想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块?