题目内容
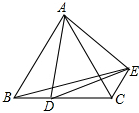 如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )
如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )A、2
| ||
B、
| ||
C、4
| ||
| D、7 |
考点:旋转的性质,等边三角形的性质
专题:计算题
分析:作EH⊥BC于H,如图,根据等边三角形的性质得BC=AB=6,∠ABC=∠ACB=60°,则BD=2,再根据旋转的性质得CE=BD=2,∠ACE=∠ABD=60°,于是根据平角的定义可计算出∠ECH=60°,接着在Rt△CEH中利用含30度的直角三角形三边的关系计算出CHH=
CE=1,EH=
CH=
,然后在Rt△BEH中利用勾股定理可计算出BE.
| 1 |
| 2 |
| 3 |
| 3 |
解答:解:作EH⊥BC于H,如图,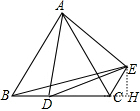
∵△ABC为等边三角形,
∴BC=AB=6,∠ABC=∠ACB=60°,
∵BC=23BD,
∴BD=2,
∵△ABD绕点A旋转后得到△ACE,
∴CE=BD=2,∠ACE=∠ABD=60°,
∴∠ECH=180°-∠ACB-∠ACE=60°,
在Rt△CEH中,∵∠CEH=30°,
∴CH=
CE=1,EH=
CH=
,
∴BH=BC+CH=7,
在Rt△BEH中,∵EH=
,BH=7,
∴BE=
=2
.
故选A.

∵△ABC为等边三角形,
∴BC=AB=6,∠ABC=∠ACB=60°,
∵BC=23BD,
∴BD=2,
∵△ABD绕点A旋转后得到△ACE,
∴CE=BD=2,∠ACE=∠ABD=60°,
∴∠ECH=180°-∠ACB-∠ACE=60°,
在Rt△CEH中,∵∠CEH=30°,
∴CH=
| 1 |
| 2 |
| 3 |
| 3 |
∴BH=BC+CH=7,
在Rt△BEH中,∵EH=
| 3 |
∴BE=
| EH2+BH2 |
| 13 |
故选A.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.运用含30度的直角三角形三边的关系和勾股定理也是解决问题的关键.

练习册系列答案
相关题目
a是不等于b的任何实数,关于x的方程是(a-b)x2+(c-b)x+c-a=0总有一个根等于( )
| A、1 | B、-1 | C、0 | D、2 |
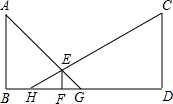 如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由.
如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由. 如图所示的几何体是由5个相同的小正方体搭成的,请画出它的主视图、左视图和俯视图.
如图所示的几何体是由5个相同的小正方体搭成的,请画出它的主视图、左视图和俯视图.