题目内容
8. 如图,已知AOB是一条直线,OC平分∠DOB,OE⊥OC.求证:OE平分∠AOD.
如图,已知AOB是一条直线,OC平分∠DOB,OE⊥OC.求证:OE平分∠AOD.
分析 根据角平分线的性质可得∠DOC=∠BOC,根据OE⊥OC和平角的性质,可得∠DOE+∠DOC=90°,∠BOC+∠AOE=90°,根据余角的性质可得∠DOE=∠AOE,即可证明OE平分∠AOD.
解答 证明:∵OC平分∠BOD,
∴∠DOC=∠BOC,
∵OE⊥OC,
∴∠DOE+∠DOC=90°,∠BOC+∠AOE=90°,
∴∠DOE=∠AOE,
∴OE平分∠AOD.
点评 本题考查了角平分线的定义、余角和补角的知识,解答本题的关键是理解余角的定义,掌握角平分线的性质.

练习册系列答案
相关题目
18. 如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )
如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )
 如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )
如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )| A. | 线段BD | B. | 线段CD | C. | 线段AC | D. | 线段BC |
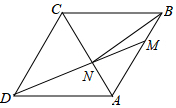 如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN
如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN 如图,已知△ABC.
如图,已知△ABC.