题目内容
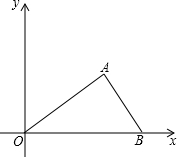 已知B(10,0),OA=5,sin∠AOB=
已知B(10,0),OA=5,sin∠AOB=| 3 |
| 5 |
考点:解直角三角形,坐标与图形性质
专题:
分析:作AC⊥x轴于C,先在Rt△AOC中,利用正弦函数的定义求出AC=OA•sin∠AOC=3,根据勾股定理求出OC=
=4,得到点A的坐标是(4,3).再由B(10,0)求出BC=OB-OC=6,然后在Rt△ABC中根据勾股定理求出AB=
=3
,利用正弦函数的定义求出sin∠ABO=
=
.
| OA2-AC2 |
| AC2+BC2 |
| 5 |
| AC |
| AB |
| ||
| 5 |
解答: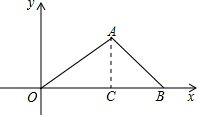 解:作AC⊥x轴于C,如图,
解:作AC⊥x轴于C,如图,
在Rt△AOC中,∵∠ACO=90°,OA=5,sin∠AOC=
,
∴AC=OA•sin∠AOC=5×
=3,
∴OC=
=4,
∴点A的坐标是(4,3).
∵OB=10,
∴BC=OB-OC=6,
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=6,
∴AB=
=3
,
∴sin∠ABO=
=
=
.
 解:作AC⊥x轴于C,如图,
解:作AC⊥x轴于C,如图,在Rt△AOC中,∵∠ACO=90°,OA=5,sin∠AOC=
| 3 |
| 5 |
∴AC=OA•sin∠AOC=5×
| 3 |
| 5 |
∴OC=
| OA2-AC2 |
∴点A的坐标是(4,3).
∵OB=10,
∴BC=OB-OC=6,
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=6,
∴AB=
| AC2+BC2 |
| 5 |
∴sin∠ABO=
| AC |
| AB |
| 3 | ||
3
|
| ||
| 5 |
点评:本题考查了解直角三角形,锐角三角函数的定义,勾股定理.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
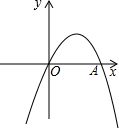 如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点.
如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点. 求阴影部分的面积 (单位:m)
求阴影部分的面积 (单位:m)