题目内容
1. 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是相等且平行.
(3)作直线MN,将△ABC分成两个面积相等的三角形.
分析 (1)作出A、B、C的对应点A′、B′、C′即可;
(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行;
(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.
解答 解:(1)平移后的△A′B′C′如图所示.
(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行,
故答案为相等且平行.
(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.
点评 本题考查平移变换、平移变换的性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12.今年我市有近3千名考生参加中考,为了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这200名考生是总体的一个样本 | B. | 近3千名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 200名学生是样本容量 |
16.下列等式成立的是( )
| A. | $\frac{1}{a}+\frac{2}{b}=\frac{3}{a+b}$ | B. | $\frac{ab}{{ab-{b^2}}}=\frac{a}{a-b}$ | C. | $\frac{2}{2a+b}=\frac{1}{a+b}$ | D. | $\frac{a}{-a+b}=-\frac{a}{a+b}$ |
 看图并按要求解决问题:
看图并按要求解决问题: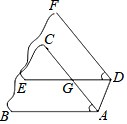 如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.
如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°. 如图,已知线段a,b,求作△ABC,使底BC=a,底边BC上的高线为b.(保留作图痕迹,不要求写作法).
如图,已知线段a,b,求作△ABC,使底BC=a,底边BC上的高线为b.(保留作图痕迹,不要求写作法).