题目内容
11.(1)已知:a、b互为相反数,cd=1,|x|=2,求a+b-cd+|x|的值;(2)求a2+b2-(a-b)2的值,其中a=$\frac{1}{2}$,b=-2.
分析 (1)由a、b互为相反数,推出a+b=0,由此即可解决问题.
(2)利用完全平方公式展开,合并同类项化简后代入计算即可.
解答 解;(1)∵a、b互为相反数,
∴a+b=0,
∵cd=1,|x|=2,
∴a+b-cd+|x|=0-1+2=1.
(2)∵a=$\frac{1}{2}$,b=-2,
∴a2+b2-(a-b)2=2ab=2×$\frac{1}{2}$×(-2)=-2.
点评 本题考查代数式求值,完全平方公式,相反数的性质等知识,解题的关键是熟练掌握乘法公式,记住相反数的性质,属于常考常考题型.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
6.一个长方形的周长是18cm,若这个长方形的长减少1cm,宽增加2cm,就可以成为一个正方形,则此正方形的边长是( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
20.下列说法错误的是( )
| A. | 已知两边及一角只能作出唯一的三角形 | |
| B. | 到△ABC的三个顶点距离相等的点是△ABC的三条边垂直平分线的交点 | |
| C. | 腰长相等的两个等腰直角三角形全等 | |
| D. | 点A(3,2)关于x轴的对称点A坐标为(3,-2) |
 如图,是一个10×10的正方形网格,其中正方形的顶点称为格点,网格中△ABC的顶点A,B,C均在格点上,利用网格建立的平面直角坐标系中点A的坐标为(3,4).
如图,是一个10×10的正方形网格,其中正方形的顶点称为格点,网格中△ABC的顶点A,B,C均在格点上,利用网格建立的平面直角坐标系中点A的坐标为(3,4).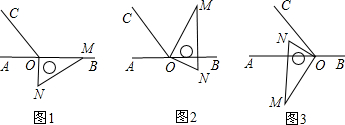
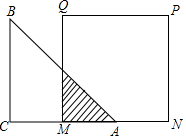 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合. 如图,以AB的中点O为位似中心,按比例尺1:2把矩形ABCD缩小.
如图,以AB的中点O为位似中心,按比例尺1:2把矩形ABCD缩小.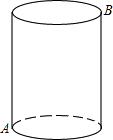 如图,一个有盖的圆柱形糖罐,一粒砂糖落在了点B的位置,一只蚂蚁刚好在圆柱点A处,蚂蚁想吃到砂糖,怎么走最近?如果糖罐变成了正方体、长方体,问题又怎么解决?如果砂糖没有掉在B处,或者蚂蚁跑到了其他点的位置,解决方法还一样吗?
如图,一个有盖的圆柱形糖罐,一粒砂糖落在了点B的位置,一只蚂蚁刚好在圆柱点A处,蚂蚁想吃到砂糖,怎么走最近?如果糖罐变成了正方体、长方体,问题又怎么解决?如果砂糖没有掉在B处,或者蚂蚁跑到了其他点的位置,解决方法还一样吗? 如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,16),D(0,-4),则线段AB的长度为( )
如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,16),D(0,-4),则线段AB的长度为( )