题目内容
 在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为
在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为考点:菱形的性质,翻折变换(折叠问题)
专题:
分析:利用翻折变换的性质以及相似三角形的判定与性质得出△BCF∽△GDC以及△GEC∽△CED,再求出CE2=EG•ED进而得出答案.
解答: 解:∵∠A=∠DGF,∠A+∠B=180°,∠DGF+∠DGC=180°,
解:∵∠A=∠DGF,∠A+∠B=180°,∠DGF+∠DGC=180°,
∴∠CBF=∠DGC,
∵AB∥CD,
∴∠BFC=∠DCG,
∴△BCF∽△GDC,
∴∠GCE=∠CDE,
∵∠GEC=∠CED,
∴△GEC∽△CED,
∴
=
,
即CE2=EG•ED,
∵DG=AD=CD,
∴∠DGC=∠DCG,
∴∠CFB=∠CBF,
∴BC=CF=4,
∴CE=2,
∴22=GE(GE+4),
解得:GE=2
-2.
故答案为:2
-2.
 解:∵∠A=∠DGF,∠A+∠B=180°,∠DGF+∠DGC=180°,
解:∵∠A=∠DGF,∠A+∠B=180°,∠DGF+∠DGC=180°,∴∠CBF=∠DGC,
∵AB∥CD,
∴∠BFC=∠DCG,
∴△BCF∽△GDC,
∴∠GCE=∠CDE,
∵∠GEC=∠CED,
∴△GEC∽△CED,
∴
| CE |
| ED |
| EG |
| CE |
即CE2=EG•ED,
∵DG=AD=CD,
∴∠DGC=∠DCG,
∴∠CFB=∠CBF,
∴BC=CF=4,
∴CE=2,
∴22=GE(GE+4),
解得:GE=2
| 2 |
故答案为:2
| 2 |
点评:此题主要考查了菱形的性质以及相似三角形的判定与性质,得出△GEC∽△CED是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果零上5℃记作+5℃,那么零下10℃记作( )
| A、-5 | B、-10 |
| C、-10℃ | D、-5℃ |
下列命题是假命题的是( )
| A、不在同一直线上的三点确定一个圆 |
| B、矩形的四个顶点在同一个圆上 |
| C、三角形的内心到三角形三边的距离相等 |
| D、平分弦的直径垂直于弦 |
下列语句中正确的是( )
| A、平分弦的直径垂直于弦 |
| B、过圆心的线段叫圆的直径 |
| C、相等的圆心角所对弧相等 |
| D、在同一圆中,相等的弧所对圆心角相等 |
 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=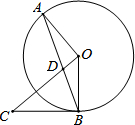 如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.
如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.