题目内容
18.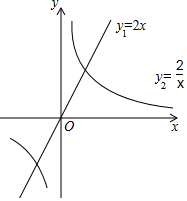 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<-1.”你同意他的观点吗?
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<-1.”你同意他的观点吗?答:不同意.理由是解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
所以直线y1=2x与双曲线y2=$\frac{2}{x}$的图象的两个交点坐标为(-1,-2),(1,2),
所以当x<-1或0<x<1时,y1<y2.
分析 先解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$得直线y1=2x与双曲线y2=$\frac{2}{x}$的图象的两个交点坐标为(-1,-2),(1,2),然后利用函数图象,写出反比例函数图象在一次函数图象上方所对应的自变量的范围可判断小明的观点不正确.
解答 解:不同意,理由如下:
解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
所以直线y1=2x与双曲线y2=$\frac{2}{x}$的图象的两个交点坐标为(-1,-2),(1,2),
所以当x<-1或0<x<1时,y1<y2.
故答案为不同意;解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,所以直线y1=2x与双曲线y2=$\frac{2}{x}$的图象的两个交点坐标为(-1,-2),(1,2),当x<-1或0<x<1时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

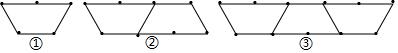
(1)若按这样的规律摆下去,请把表格补充完整:
| 图形标号 | ① | ② | ③ | ④ | ⑤ | … | n | … |
| 火柴棒数 | 5 | 9 | 13 | 17 | 21 | … | 4n+1 | … |
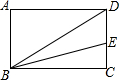 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 3 | D. | 4 |

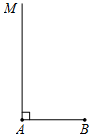 尺规作图
尺规作图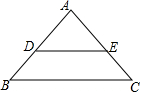 如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )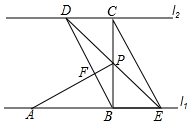 如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.
如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.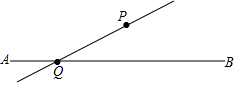 如图,按要求作图:
如图,按要求作图: