题目内容
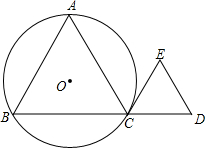 已知点C是线段BD上一动点,分别以线段BC和线段DC为边在BD同侧作等边△ABC和等边△CDE,⊙O是△ABC的外接圆.
已知点C是线段BD上一动点,分别以线段BC和线段DC为边在BD同侧作等边△ABC和等边△CDE,⊙O是△ABC的外接圆.(1)如图,求证:CE为⊙O的切线;
(2)若△CDE的边DE所在直线恰好与圆O相切,线段BD=4,求圆O的半径.
考点:切线的判定,等边三角形的性质
专题:
分析:(1)连结OC,根据等边三角形的性质得∠ACB=∠ECD=60°,则∠ACE=60°,再根据等边三角形的内外心重合得到∠ACO=30°,则∠OCE=90°,然后根据切线的判定定理即可得到结论;
(2)作OH⊥BC于H,连结OF、OC、FC,根据垂径定理得BH=CH,设OH=a,则CH=
a,OC=2a,所以BC=2
a,OF⊥FD,由△CDE为等边三角形得∠CED=60°,∠D=60°,则∠CEF=120°,易得∠COF=60°,于是可判断△OCF为等边三角形,根据等边三角形的性质得∠OFC=60°,FC=OC=2a,可计算出∠CFD=30°,则∠FCD=90°,由此得到CD=
FC=
a,根据BD=4,得出a的值,即可得出圆O的半径OC.
(2)作OH⊥BC于H,连结OF、OC、FC,根据垂径定理得BH=CH,设OH=a,则CH=
| 3 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答: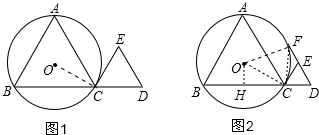 (1)证明:连结OC,如图1,
(1)证明:连结OC,如图1,
∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,
∴∠ACE=60°,
∵⊙O是等边△ABC的外接圆,
∴点O是等边△ABC的外心和内心,
∴∠ACO=
∠ACB=30°,
∴∠OCE=30°+60°=90°,
∴OC⊥CE,
∴CE为⊙O的切线;
(2)解:作OH⊥BC于H,连结OF、OC、FC,如图2,
∵OH⊥BC,
∴BH=CH,
设OH=a,则CH=
a,OC=2a,
∴BC=2
a,
∵DF与⊙O切于点F,
∴OF⊥FD,
∵△CDE为等边三角形,
∴∠CED=60°,∠D=60°,
∴∠CEF=120°,
而∠OCE=∠OFE=90°,
∴∠COF=60°,
∴△OCF为等边三角形,
∴∠OFC=60°,FC=OC=2a,
∴∠CFD=30°,
∴∠FCD=90°,
∴CD=
FC=
a,
∵BD=4,
∴CD+BC=4,
∴
a+2
a=4,
∴a=
,
∴OC=2a=
.
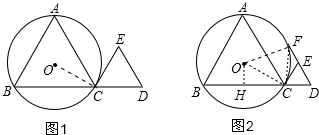 (1)证明:连结OC,如图1,
(1)证明:连结OC,如图1,∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,
∴∠ACE=60°,
∵⊙O是等边△ABC的外接圆,
∴点O是等边△ABC的外心和内心,
∴∠ACO=
| 1 |
| 2 |
∴∠OCE=30°+60°=90°,
∴OC⊥CE,
∴CE为⊙O的切线;
(2)解:作OH⊥BC于H,连结OF、OC、FC,如图2,
∵OH⊥BC,
∴BH=CH,
设OH=a,则CH=
| 3 |
∴BC=2
| 3 |
∵DF与⊙O切于点F,
∴OF⊥FD,
∵△CDE为等边三角形,
∴∠CED=60°,∠D=60°,
∴∠CEF=120°,
而∠OCE=∠OFE=90°,
∴∠COF=60°,
∴△OCF为等边三角形,
∴∠OFC=60°,FC=OC=2a,
∴∠CFD=30°,
∴∠FCD=90°,
∴CD=
| ||
| 3 |
2
| ||
| 3 |
∵BD=4,
∴CD+BC=4,
∴
2
| ||
| 3 |
| 3 |
∴a=
| ||
| 2 |
∴OC=2a=
| 3 |
点评:本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.也考查了垂径定理、等边三角形的判定与性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
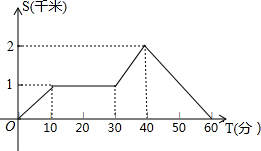 星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )
星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )| A、从家出发,休息一会,就回家 |
| B、从家出发,一直散步(没有停留),然后回家 |
| C、从家出发,休息一会,返回用时20分钟 |
| D、从家出发,休息一会,继续行走一段,然后回家 |
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
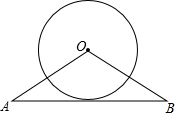 已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切.
已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切. 如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2
如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2 如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).
如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).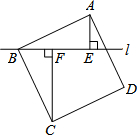 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为