题目内容
8.设二次函数y=(m-1)x2+(m-2)x-1,记其图象为C.(1)若图象C与x轴有两个公共点,求实数m的取值范围;
(2)求证:图象C恒过x轴上的定点,并求该定点的坐标;
(3)若图象C上所有点均在直线y=mx+1的下方,求实数m的取值范围.
分析 (1)由二次函数的定义可知m-1≠0,然后再根据△>0列不等式求解即可;
(2)将(m-1)x2+(m-2)x-1分解分式,从而可判断C横过点(-1,0);
(3)根据题意可知m-1<0,且方程y=mx+1与方程y=(m-1)x2+(m-2)x-1无公共点.
解答 解:(1)由二次函数的定义可知m-1≠0,
∴m≠1.
∵图象C与x轴有两个公共点,
∴方程(m-1)x2+(m-2)x-1=0有两个不相等的实数根.
∴(m-2)2+4(m-1)>0.
解得:m≠0.
∴m的取值范围是m≠0且m≠1.
(2)令y=0得:(m-1)x2+(m-2)x-1=0
∴[(m-1)x-1](x+1)=0.
∴当x=-1,y=0.
∴无论m取何值函数图象横过点(-1,0).
(3)根据题意可知:m-1<0,且y=mx+1与y=(m-1)x2+(m-2)x-1无公共点.
由m-1<0得m<1.
由方程y=mx+与1y=(m-1)x2+(m-2)x-1无公共点可知:方程(m-1)x2+(m-2)x-1-mx-1=0无解.
整理得:(m-1)x2-2x-2=0.
∴4+8(m-1)<0.
解得:m<$\frac{1}{2}$.
∴m的取值范围是m$<\frac{1}{2}$.
点评 本题主要考查的二次函数与x轴的交点问题,将函数问题转化为方程、不等式问题是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
20.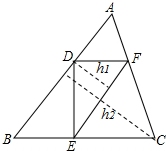 如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )
如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )
 如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )
如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
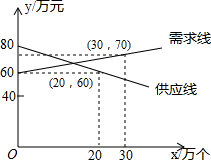 某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?
某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡? 如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3.
如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3. 在△ABC中,点D是BC的中点.
在△ABC中,点D是BC的中点.