题目内容
13. 如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3.
如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3.
分析 作AH⊥BC于H,延长CA交⊙A于F,连接BF,根据已知条件得到∠DAE=∠BAF,得到$\widehat{DE}$=$\widehat{BF}$,求得DE=BF=6,由垂径定理得到CH=BH,然后根据三角形的中位线即可得到结论.
解答  解:作AH⊥BC于H,延长CA交⊙A于F,连接BF,
解:作AH⊥BC于H,延长CA交⊙A于F,连接BF,
∵∠BAC+∠EAD=180°,
∵∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴$\widehat{DE}$=$\widehat{BF}$,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵AC=AF,
∴AH=$\frac{1}{2}$BF=3.
故答案为:3.
点评 本题考查了圆周角定理.三角形的中位线的性质,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目


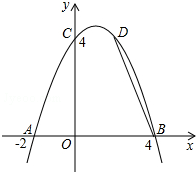 如图,已知抛物线y=ax2+bx+c经过A(-2,0)、B(4,0)、C(0,4)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0)、B(4,0)、C(0,4)三点. 如图,已知:AB∥DE,AB=DE,∠1=∠2,求证:FC=GC.
如图,已知:AB∥DE,AB=DE,∠1=∠2,求证:FC=GC.