题目内容
1.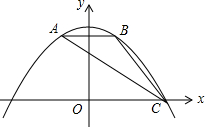 如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
分析 (1)易得抛物线的顶点为(0,$\frac{9}{4}$),然后只需运用待定系数法,就可求出抛物线的函数关系表达式;
(2)①当点F在第一象限时,如图1,可求出点C的坐标,直线AC的解析式,设正方形OEFG的边长为p,则F(p,p),代入直线AC的解析式,就可求出点F的坐标;②当点F在第二象限时,同理可求出点F的坐标,此时点F不在线段AC上,故舍去;
(3)过点M作MH⊥DN于H,如图2,由题可得0≤t≤2.然后只需用t的式子表示DN、DM2、MN2,分三种情况(①DN=DM,②ND=NM,③MN=MD)讨论就可解决问题.
解答 解:(1)∵点B是点A关于y轴的对称点,
∴抛物线的对称轴为y轴,
∴抛物线的顶点为(0,$\frac{9}{4}$),
故抛物线的解析式可设为y=ax2+$\frac{9}{4}$.
∵A(-1,2)在抛物线y=ax2+$\frac{9}{4}$上,
∴a+$\frac{9}{4}$=2,
解得a=-$\frac{1}{4}$,
∴抛物线的函数关系表达式为y=-$\frac{1}{4}$x2+$\frac{9}{4}$;
(2)①当点F在第一象限时,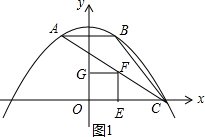 如图1,
如图1,
令y=0得,-$\frac{1}{4}$x2+$\frac{9}{4}$=0,
解得:x1=3,x2=-3,
∴点C的坐标为(3,0).
设直线AC的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{-m+n=2}\\{3m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=\frac{3}{2}}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$.
设正方形OEFG的边长为p,则F(p,p).
∵点F(p,p)在直线y=-$\frac{1}{2}$x+$\frac{3}{2}$上,
∴-$\frac{1}{2}$p+$\frac{3}{2}$=p,
解得p=1,
∴点F的坐标为(1,1).
②当点F在第二象限时,
同理可得:点F的坐标为(-3,3),
此时点F不在线段AC上,故舍去.
综上所述:点F的坐标为(1,1);
(3)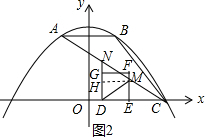 过点M作MH⊥DN于H,如图2,
过点M作MH⊥DN于H,如图2,
则OD=t,OE=t+1.
∵点E和点C重合时停止运动,∴0≤t≤2.
当x=t时,y=-$\frac{1}{2}$t+$\frac{3}{2}$,则N(t,-$\frac{1}{2}$t+$\frac{3}{2}$),DN=-$\frac{1}{2}$t+$\frac{3}{2}$.
当x=t+1时,y=-$\frac{1}{2}$(t+1)+$\frac{3}{2}$=-$\frac{1}{2}$t+1,则M(t+1,-$\frac{1}{2}$t+1),ME=-$\frac{1}{2}$t+1.
在Rt△DEM中,DM2=12+(-$\frac{1}{2}$t+1)2=$\frac{1}{4}$t2-t+2.
在Rt△NHM中,MH=1,NH=(-$\frac{1}{2}$t+$\frac{3}{2}$)-(-$\frac{1}{2}$t+1)=$\frac{1}{2}$,
∴MN2=12+($\frac{1}{2}$)2=$\frac{5}{4}$.
①当DN=DM时,
(-$\frac{1}{2}$t+$\frac{3}{2}$)2=$\frac{1}{4}$t2-t+2,
解得t=$\frac{1}{2}$;
②当ND=NM时,
-$\frac{1}{2}$t+$\frac{3}{2}$=$\sqrt{\frac{5}{4}}$=$\frac{\sqrt{5}}{2}$,
解得t=3-$\sqrt{5}$;
③当MN=MD时,
$\frac{5}{4}$=$\frac{1}{4}$t2-t+2,
解得t1=1,t2=3.
∵0≤t≤2,∴t=1.
综上所述:当△DMN是等腰三角形时,t的值为$\frac{1}{2}$,3-$\sqrt{5}$或1.
点评 本题主要考查了运用待定系数法求抛物线及直线的解析式、直线及抛物线上点的坐标特征、抛物线的性质、解一元二次方程、勾股定理等知识,运用分类讨论的思想是解决第(2)、(3)小题的关键,在解决问题的过程中要验证是否符合题意.

| A. | 22或25 | B. | 25 | C. | 22 | D. | 21 |
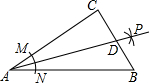 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )| A. | 15 | B. | 30 | C. | 45 | D. | 60 |
| A. | 把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 | |
| B. | 木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理 | |
| C. | 将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”的原理 |
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |

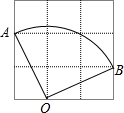 如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.