题目内容
9.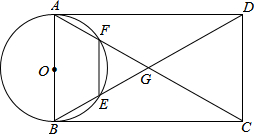 平行四边形ABCD两条对角线交于点G,∠DBC=∠ACB,以AB为直径作⊙O,分别交BD、AC于点E、点F,点E、点F分别是$\widehat{AB}$的三等分点,当BC=6时,求EF的长.
平行四边形ABCD两条对角线交于点G,∠DBC=∠ACB,以AB为直径作⊙O,分别交BD、AC于点E、点F,点E、点F分别是$\widehat{AB}$的三等分点,当BC=6时,求EF的长.
分析 根据圆心角、弧、弦的关系求出∠AOF=∠EOF=∠BOE=60°,求出△AOF和△FOE都是等边三角形,根据等边三角形的性质得出EF=OF=OA=$\frac{1}{2}$AB,∠OAF=60°,解直角三角形求出AB即可.
解答 解:如图:
连接OF、OE,
∵点E、点F分别是$\widehat{AB}$的三等分点,
∴∠AOF=∠EOF=∠BOE=60°,
∵OA=OB=OE=OF,
∴△AOF和△FOE都是等边三角形,
∴F=OF=OA=$\frac{1}{2}$AB,∠OAF=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵BC=6,
∴AB=$\frac{BC}{tan60°}$=$\frac{6}{\sqrt{3}}$=2$\sqrt{3}$,
∴EF=OA=$\frac{1}{2}$AB=$\sqrt{3}$.
点评 本题考查了矩形的性质,圆心角、弧、弦的关系,等边三角形的性质和判定,解直角三角形的应用,解此题的关键是求出EF=$\frac{1}{2}$AB和求出AB的长,难度适中.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
18.《世界保护益鸟公约》规定每年的4月1日为“国际爱鸟日”.因为有 它们,给我们的生活增添了靓丽的光彩.鸟类最昌盛的时期,约有160万种,用科学记数法可表示为( )
| A. | 1.6×105 | B. | 1.6×106 | C. | 1.6×107 | D. | 1.6×108 |
19.-$\frac{1}{5}$的倒数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
 如图,A、B两地之间有一座山,火车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,火车沿直线AB行驶.已知AC=200千米,∠A=30°,∠B=45°,则隧道开通后,火车从A地到B地比原来少走多少千米(结果保留整数,$\sqrt{2}≈1.414,\sqrt{3}$≈1.732)?
如图,A、B两地之间有一座山,火车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,火车沿直线AB行驶.已知AC=200千米,∠A=30°,∠B=45°,则隧道开通后,火车从A地到B地比原来少走多少千米(结果保留整数,$\sqrt{2}≈1.414,\sqrt{3}$≈1.732)?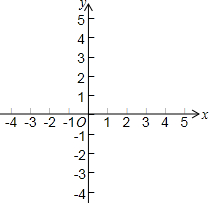 利用函数图象解方程组$\left\{\begin{array}{l}{3x+2y=5}\\{2x-y=1}\end{array}\right.$.
利用函数图象解方程组$\left\{\begin{array}{l}{3x+2y=5}\\{2x-y=1}\end{array}\right.$.