Question

根据题意结合图形填空：已知：如图，AD⊥BC于D，EG⊥BC与G，AE=AF，试问：AD是∠BAC的平分线吗？若是，请说明理由．
答：是，理由如下：
∵AD⊥BC，EG⊥BC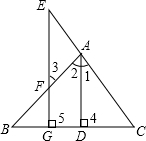（已知）
∴∠4=∠5=90°（垂直定义）
∴

 

∥

 

（　　）
∴∠2=

 

（　　）
∠1=

 

（　　）
又∵AE=AF（已知）
∴∠3=

 

（　　）
∴∠1=∠2（等量代换）
∴AD平分∠BAC（角平分线定义）

Answer 1

考点：平行线的判定与性质,垂线

专题：推理填空题

分析：根据角平分线定义得出角相等，推出AD∥EG，根据平行线的性质得出∠2=∠3，∠1=∠E，根据等腰三角形性质得出∠3=∠E，推出∠1=∠2即可．

解答：解：∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（垂直定义），
∴AD∥EG（同位角相等，两直线平行），
∴∠2=∠3（两直线平行，内错角相等），
∠1=∠E（两直线平行，同位角相等），
∵AE=AF，
∴∠3=∠E（等边对等角），
∴∠1=∠2（等量代换），
∴AD平分∠BAC（角平分线定义），
故答案为：AD，EG，∠3，∠E，∠E．

点评：本题考查了平行线的性质和判定，等腰三角形的性质，垂直定义，角平分线定义的应用，主要考查学生的推理能力，题目比较好，难度适中．