题目内容
10.已知等边三角形的边长为x,则用边长x表示等边三角形的面积y的函数表达式为$y=\frac{{\sqrt{3}}}{4}{x^2}$.分析 作出三角形的高,利用直角三角形的性质及勾股定理可得高,那么三角形的面积=$\frac{1}{2}$×底×高,把相关数值代入即可求解.
解答 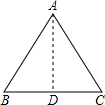 解:作等边三角形ABC中BC边上的高AD.
解:作等边三角形ABC中BC边上的高AD.
∵△ABC是等边三角形,边长为x,
∴CD=$\frac{1}{2}$x,
∴高AD=$\frac{\sqrt{3}}{2}$x,
∴△ABC的面积=$\frac{1}{2}$BC•AD,
即y=$\frac{1}{2}$x•$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{4}$x2.
故答案为y=$\frac{\sqrt{3}}{4}$x2.
点评 本题考查了根据实际问题列二次函数关系式,勾股定理,三角形的面积,用含x的代数式表示出等边三角形一边上的高是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列各数中,没有平方根的是( )
| A. | 4 | B. | 0 | C. | $\frac{1}{8}$ | D. | -9 |
18.若一个三角形成轴对称图形,且有一个内角为60°,则这个三角形一定是( )
| A. | 直角三角形 | B. | 等腰直角三角形 | ||
| C. | 等边三角形 | D. | 底和腰不相等的等腰三角形 |
 已知二次函数y=x2+bx+c的图象经过点(1,0)、(4,3).
已知二次函数y=x2+bx+c的图象经过点(1,0)、(4,3).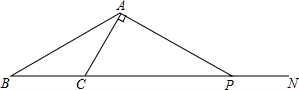 如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.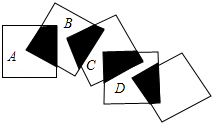 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.