题目内容
2.解方程组:(1)$\left\{\begin{array}{l}{3x-2y=13}\\{2x+y=4}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x-3y}{4}+\frac{y+5}{3}=2x-7}\\{10(x-y)-4(1-x)=3y}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-2y=13①}\\{2x+y=4②}\end{array}\right.$,
①+②×2得:7x=21,
解得:x=3,
把x=3代入②得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{21x+5y=104①}\\{14x-13y=4②}\end{array}\right.$,
①×13+②×5得:343x=1372,即x=4,
把x=4代入②得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
17.函数y=$\frac{\sqrt{x+3}}{x-1}$中自变量x的取值范围是( )
| A. | x≥-3 | B. | x≥-3且x≠1 | C. | x≠1 | D. | x≠-3且x≠1 |
 尺规作图,不写作法,保留作图痕迹.
尺规作图,不写作法,保留作图痕迹.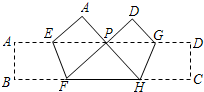 如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.
如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.