题目内容
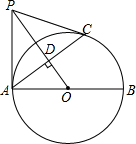 如图,AB是⊙O的直径,C是圆周上一点,OD⊥AC于点D.过C作⊙O的切线,交OD的延长线于点P,连接AP.
如图,AB是⊙O的直径,C是圆周上一点,OD⊥AC于点D.过C作⊙O的切线,交OD的延长线于点P,连接AP.(1)求证:AP是⊙O的切线.
(2)若
| AC |
| AB |
| 4 |
| 5 |
| 16 |
| 3 |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)首先连接OC,易证得△AOP≌△COP(SAS),可得∠PAO=∠PCO,又由PC是⊙O的切线,易证得OA⊥PA,即可证得AP是⊙O的切线.
(2)首先连接BC,由
=
,易证得
=
,可设CD=4k,则CO=5k,OD=3k,易证得△CPD∽△OCD,然后由相似三角形的对应边成比例,求得PD=
k,又由PD=
,即可求得答案.
(2)首先连接BC,由
| AC |
| AB |
| 4 |
| 5 |
| CD |
| CO |
| 4 |
| 5 |
| 16 |
| 3 |
| 16 |
| 3 |
解答:(1)证明:连接OC.
∵AC是⊙O的弦,OD⊥AC,OA=OC,
∴∠AOP=∠COP,
在△AOP和△COP中,
,
∴△AOP≌△COP(SAS),
∴∠PCO=∠PAO,
∵PC切⊙O于点C,
 ∴OC⊥PC,
∴OC⊥PC,
∴∠PCO=90°,
∴∠PAO=90°,
即OA⊥PA,
又∵OA是⊙O的半径,
∴AP是⊙O的切线;
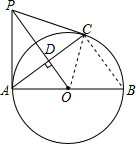
(2)连接BC.
∵AB是⊙O的直径,
∴AC⊥BC,
又∵OD⊥AC,
∴OD∥BC,
∴
=
=
,
∴
=
,
设CD=4k,则CO=5k,OD=3k.
∵∠CPD+∠COD=90°,∠COD+∠OCD=90°,
∴∠CPD=∠OCD,
∵∠PDC=∠CDO=90°,
∴△CPD∽△OCD,
∴
=
,
∴PD=
k,
∵PD=
,
∴k=1,
∴OC=5,
∴⊙O的半径长为5.
∵AC是⊙O的弦,OD⊥AC,OA=OC,
∴∠AOP=∠COP,
在△AOP和△COP中,
|
∴△AOP≌△COP(SAS),
∴∠PCO=∠PAO,
∵PC切⊙O于点C,
 ∴OC⊥PC,
∴OC⊥PC,∴∠PCO=90°,
∴∠PAO=90°,
即OA⊥PA,
又∵OA是⊙O的半径,
∴AP是⊙O的切线;
(2)连接BC.
∵AB是⊙O的直径,
∴AC⊥BC,
又∵OD⊥AC,
∴OD∥BC,
∴
| AD |
| AO |
| AC |
| AB |
| 4 |
| 5 |
∴
| CD |
| CO |
| 4 |
| 5 |
设CD=4k,则CO=5k,OD=3k.
∵∠CPD+∠COD=90°,∠COD+∠OCD=90°,
∴∠CPD=∠OCD,
∵∠PDC=∠CDO=90°,
∴△CPD∽△OCD,
∴
| CD |
| PD |
| OD |
| DC |
∴PD=
| 16 |
| 3 |
∵PD=
| 16 |
| 3 |
∴k=1,
∴OC=5,
∴⊙O的半径长为5.
点评:此题考查了切线的性质与判定、等腰三角形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
计算-1+(-1)2+(-1)3+(-1)4+…+(-1)2015的值,结果正确的是( )
| A、1 | B、-1 | C、0 | D、-1或0 |
已知一个正方形的半径为R,边心距为r,则r:R等于( )
| A、1:2 | ||
B、
| ||
C、
| ||
D、
|
 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )| A、b-a>0 | B、-b>0 |
| C、a>-b | D、-ab<0 |
从直观上看,下列线段中最长的是( )
A、 |
B、 |
C、 |
D、 |
如果抛物线y=x2+2向右平移1个单位长度,那么所得新抛物线的解析式为( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+2 |
| C、y=x2+3 |
| D、y=x2+1 |
已知
=
,那么下列式子中一定成立的是( )
| m |
| 3 |
| n |
| 4 |
| A、4m=3n | B、3m=4n |
| C、m=4n | D、mn=12 |
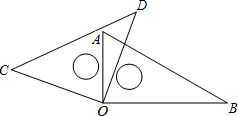 将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为
将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为