题目内容
已知一个正方形的半径为R，边心距为r，则r：R等于（ ）
| A、1：2 | ||
B、
| ||
C、
| ||
D、
|
考点：正多边形和圆
专题：
分析：运用正方形的性质，以及与外接圆的关系，分别求出中心角，边心距进而得出答案．
解答：解：∵正方形的边长为R，
由中心角只有四个可得出：
=90°，
∴中心角是：90°，
正方形的外接圆半径是：sin∠AOC=
，
∵AC=
，∠AOC=45°，
∴r=OC=
R，
∴r：R=
R：R=
：2．
故选：B．
由中心角只有四个可得出：
| 360° |
| 4 |
∴中心角是：90°，
正方形的外接圆半径是：sin∠AOC=
| AC |
| OA |
∵AC=
| R |
| 2 |
∴r=OC=
| ||
| 2 |
∴r：R=
| ||
| 2 |
| 2 |
故选：B．
点评：此题主要考查了正方形的性质与正方形与它的外接圆的关系，表示出CO的长是解题关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
下列运算错误的是（ ）
A、(-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图在平面直角坐标系中，四边形OABC的顶点分别是O（0，0），A（6，0），B（3，6），C（-3，3）．
已知线段a及∠1，用尺规作△ABC使得AC=a，AB=2a，∠A=∠1．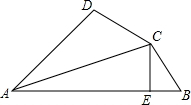
如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE-2S△BCE=S△ADC；其中正确结论的个数是（ ）
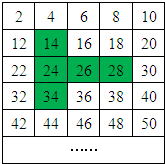如图，将连续的偶数2，4，6，8，10，…排成一数阵，有一个能够在数阵中上下左右平移的T字架，它可以框出数阵中的五个数．试判断这五个数的和能否为426？若能，请求出这五个数；若不能，请说明理由．
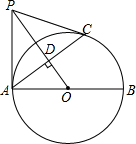如图，AB是⊙O的直径，C是圆周上一点，OD⊥AC于点D．过C作⊙O的切线，交OD的延长线于点P，连接AP．