题目内容
19．若$\frac{x}{y}$=$\frac{3}{2}$，则下列各式中成立的是（ ）| A． | $\frac{x+y}{y}$=5 | B． | $\frac{y}{x-y}$=$\frac{1}{3}$ | C． | $\frac{x+3}{y+2}$=$\frac{2}{3}$ | D． | $\frac{x-y}{x+y}$=$\frac{1}{5}$ |
分析 根据比例的性质计算后选择答案即可．
解答 解：∵$\frac{x}{y}$=$\frac{3}{2}$，
∴设x=3a，y=2a，
在D选项中，$\frac{x-y}{x+y}$=$\frac{3a-2a}{3a+2a}$=$\frac{1}{5}$，
故D选项正确．
故选D．
点评 本题主要考查了比例的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
9．为了参加市中学生篮球运动会，一支校篮球队准备购买双运动鞋，各种尺码的统计如表所示，则这双运动鞋尺码的众数和中位数分别为（ ）
| 尺码（厘米） | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量（双） | 1 | 4 | 2 | 1 | 1 |
| A． | 25.5cm 26 cm | B． | 26 cm 25.5 cm | ||
| C． | 25.5 cm 25.5 cm | D． | 26 cm 26 cm |
10．下列运算正确的是（ ）
| A． | $\frac{1}{2}$÷（-$\frac{4}{7}$）=-2 | B． | 4÷（-24）=-$\frac{1}{6}$ | C． | -18÷（-3）=-6 | D． | 6÷（-3）×（-$\frac{1}{3}$）=6 |
7．把函数y=3x+2的图象向下平移1个单位长度，所得图象的函数解析式是（ ）
| A． | y=3x+3 | B． | y=3x-1 | C． | y=3x+1 | D． | y=3x+5 |
14．已知二次函数y=（x-m）2+n图象上的两点A（m，a）和B（n，b），则a与b的大小关系是（ ）
| A． | a≥b | B． | a≤b | C． | a＞b | D． | a＜b |
8．
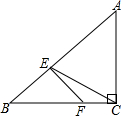如图，在△ABC中，AC=BC，∠BCA=90°，点E是斜边AB上的一点，作EF⊥AB交边BC于点F连结EC，若BE：EA=1：2，则∠ECF的余弦值为（ ）
如图，在△ABC中，AC=BC，∠BCA=90°，点E是斜边AB上的一点，作EF⊥AB交边BC于点F连结EC，若BE：EA=1：2，则∠ECF的余弦值为（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\sqrt{5}$ | D． | -$\frac{\sqrt{5}}{5}$ |
5．下列各式中，正确的是 （ ）
| A． | $±\sqrt{9}=±3$ | B． | -（$\sqrt{2}$）2=4 | C． | $\root{3}{-9}=-3$ | D． | $\sqrt{{{（-2）}^2}}=-2$ |
6．若关于x的一元二次方程（b-c）x2+（a-b）x+c-a=0有两个相等的实数根，则a、b、c之间的关系是（ ）
| A． | a=$\frac{b+c}{2}$ | B． | b=$\frac{a+c}{2}$ | C． | c=$\frac{a+b}{2}$ | D． | a+b+c=0 |