题目内容
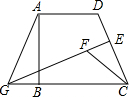 如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,
如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,(1)求证:∠GFC=∠GAD;
(2)若∠GFC=120°,GB=2
| 3 |
考点:全等三角形的判定与性质
专题:
分析:(1)连接GD,根据E为DC的中点,GF⊥CD得到GF垂直平分CD,从而得到GD=GC,然后证得△DAG≌△CFG,从而得到∠GFC=∠GAD;
(2))根据∠GFC=120°,得到∠GAD=120°,然后利用AD∥GC,得到∠AGB=60°,从而根据GB=2
得到AG=4
,最后得到GF=AG=4
.
(2))根据∠GFC=120°,得到∠GAD=120°,然后利用AD∥GC,得到∠AGB=60°,从而根据GB=2
| 3 |
| 3 |
| 3 |
解答: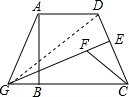 解:(1)连接GD,
解:(1)连接GD,
∵E为DC的中点,GF⊥CD,
∴GF垂直平分CD,
∴GD=GC,
在△DAG和△CFG中,
,
∴△DAG≌△CFG(SSS),
∴∠GFC=∠GAD;
(2)∵∠GFC=120°,
∴∠GAD=120°,
∵AD∥GC,
∴∠AGB=60°,
∵GB=2
,
∴AG=4
,
∴GF=AG=4
.
 解:(1)连接GD,
解:(1)连接GD,∵E为DC的中点,GF⊥CD,
∴GF垂直平分CD,
∴GD=GC,
在△DAG和△CFG中,
|
∴△DAG≌△CFG(SSS),
∴∠GFC=∠GAD;
(2)∵∠GFC=120°,
∴∠GAD=120°,
∵AD∥GC,
∴∠AGB=60°,
∵GB=2
| 3 |
∴AG=4
| 3 |
∴GF=AG=4
| 3 |
点评:本题考查了全等三角形的判定与性质,解题的关键是构造全等三角形并正确的利用判定定理进行证明,难度不大.

练习册系列答案
相关题目
 把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.
把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.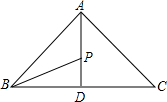 如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.
如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.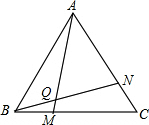 △ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.
△ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点. 如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=
如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=