题目内容
 如图,已知AB∥CD,AD和BC相交于点O,AO=DO,
如图,已知AB∥CD,AD和BC相交于点O,AO=DO,| AO |
| m |
| BO |
| n |
(1)用含
| m |
| n |
| CD |
(2)求作:
| m |
| n |
考点:*平面向量
专题:
分析:(1)由AB∥CD,易得△AOB∽△DOC,又由AO=DO,可得
=
,又由
=
,
=
,根据三角形法则即可求得答案;
(2)由△AOB∽△DOC,易得
=
=
,根据三角形法则即可求得
=
+
.
| CD |
| AB |
| AO |
| m |
| BO |
| n |
(2)由△AOB∽△DOC,易得
| OC |
| BO |
| n |
| AC |
| m |
| n |
解答:解:(1)∵
=
,
=
,
∴
=
-
=
-
,
∵AB∥CD,
∴△AOB∽△DOC,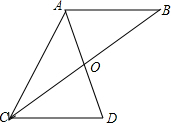
∴AB:CD=AO:DO,
∵AO=DO,
∴CD=AB,
∴
=
-
;
(2)如图,
即为所求.
理由:∵△AOB∽△DOC,
∴BO:CO=AO:DO,
∴BO=CO,
∴
=
=
,
∴
=
+
=
+
.
| AO |
| m |
| BO |
| n |
∴
| AB |
| AO |
| BO |
| m |
| n |
∵AB∥CD,
∴△AOB∽△DOC,

∴AB:CD=AO:DO,
∵AO=DO,
∴CD=AB,
∴
| CD |
| m |
| n |
(2)如图,
| AC |
理由:∵△AOB∽△DOC,
∴BO:CO=AO:DO,
∴BO=CO,
∴
| OC |
| BO |
| n |
∴
| AC |
| AO |
| OC |
| m |
| n |
点评:此题考查了平面向量的知识.此题难度适中,注意掌握三角形法则的应用,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
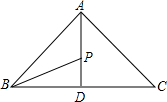 如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.
如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.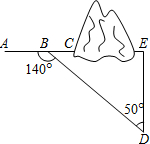 如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位)?
如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位)? 函数y=
函数y=