题目内容
13.已知二次函数抛物线的图象顶点坐标为(-2,3),且过点(1,0),(1)求此二次函数的解析式;
(2)试判断(-5,4)在不在该抛物线上,并说明理由;
(3)请说明x在什么范围内取值时,函数值y随x的增大而增大?
分析 (1)设顶点式y=a(x+2)2+3,然后把(1,0)代入求出a即可;
(2)计算x=-5所对应的函数值,然后根据二次函数图象上点的坐标特征进行判断;
(3)根据二次函数的性质求解.
解答 解:(1)设抛物线解析式为y=a(x+2)2+3,
把(1,0)代入得9a+3=0,解得a=-$\frac{1}{3}$,
所以抛物线解析式为y=-$\frac{1}{3}$(x+2)2+3;
(2)当x=-5时,y=-$\frac{1}{3}$(x+2)2+3=-$\frac{1}{3}$×9+3=9,
所以点(-5,4)不在该抛物线上;
(3)当x<-2时,函数值y随x的增大而增大.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 有理数a,b,c表示的点在数轴上的位置如图所示,
有理数a,b,c表示的点在数轴上的位置如图所示, 小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.
小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.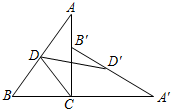 如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长.
如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长.