题目内容
8.如图,已知,线段AB=20cm,E为AB的中点,C为AB上一点,D为AB延长线上的点,且CD=4cm,B为CD的中点.求线段EC和ED的长.
分析 根据线段中点的定义得出BE=$\frac{1}{2}$AB,由于B为CD的中点于是得出BC=BD=2,进而可得出结论.
解答 解:∵线段AB=20cm,E为AB的中点,
∴BE=$\frac{1}{2}$AB=10cm.
∵CD=4cm,B为CD的中点,
∴BC=BD=2cm,
∴EC=EB-BC=10-2=8cm;
ED=EB+BD=10+2=12cm.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
16.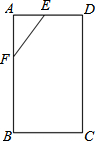 工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
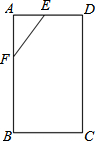 工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )| A. | 两点之间线段最短 | B. | 三角形的稳定性 | ||
| C. | 垂线段最短 | D. | 两直线平行,内错角相等 |
3.下列几何体中,属于锥体的有( )
| A. |  | B. |  | C. |  | D. |  |
17.下列各数中最小的数是( )
| A. | -3 | B. | 3 | C. | 0 | D. | -$\frac{1}{3}$ |
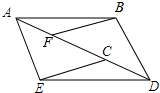 如图,AB∥ED,点F、C在AD上,AB=DE,AF=DC,试说明BC=EF.
如图,AB∥ED,点F、C在AD上,AB=DE,AF=DC,试说明BC=EF. 如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作向量2$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.
如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作向量2$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.