题目内容
20.在Rt△ABC中,∠ACB=90°,sinB=$\frac{2}{7}$,则cosB=$\frac{\sqrt{45}}{7}$;若$\sqrt{3}tan2θ=1$,则θ=15°.分析 根据sin2α+cos2α=1,可得答案;根据特殊角三角函数值,可得2θ.
解答 解:在Rt△ABC中,∠ACB=90°,sinB=$\frac{2}{7}$,
则cosB=$\sqrt{1-si{n}^{2}β}$=$\sqrt{1-(\frac{2}{7})^{2}}$=$\frac{\sqrt{45}}{7}$;
由$\sqrt{3}tan2θ=1$,得
tan2θ=$\frac{\sqrt{3}}{3}$,
2θ=30°,
θ=15°.
故答案为:$\frac{\sqrt{45}}{7}$,15°.
点评 本题考查了同角三角函数关系,利用了sin2α+cos2α=1,熟记特殊角三角函数值是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
10.下列式子化简不正确的是( )
| A. | +(-5)=-5 | B. | -(-0.5)=0.5 | C. | -|+3|=-3 | D. | -(+1$\frac{1}{2}$)=1$\frac{1}{2}$ |
11.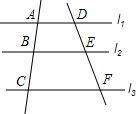 如图,l1∥l2∥l3,则下列等式错误的是( )
如图,l1∥l2∥l3,则下列等式错误的是( )
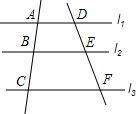 如图,l1∥l2∥l3,则下列等式错误的是( )
如图,l1∥l2∥l3,则下列等式错误的是( )| A. | $\frac{BC}{AC}=\frac{EF}{DF}$ | B. | $\frac{AB}{AC}=\frac{DE}{DF}$ | C. | $\frac{AB}{DE}=\frac{BC}{EF}$ | D. | $\frac{AB}{AC}=\frac{AD}{CF}$ |
10.如图,数轴上A,B两点分别对应有理数a,b,则a,-a,b,-b,1比较大小正确的是( )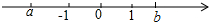
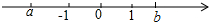
| A. | a<-a<b<-b<1 | B. | a<-b<b<1<-a | C. | a<b<-a<-b<1 | D. | a<-b<1<b<-a |

 如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=20°,∠E=110°,∠EAB=15°,则∠BAD的度数为65°.
如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=20°,∠E=110°,∠EAB=15°,则∠BAD的度数为65°.