题目内容
19．
如图，已知向量$\overrightarrow{a}$、$\overrightarrow{b}$，求作向量2$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$．
分析 首先画出$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{b}$，$\overrightarrow{BC}$=2$\overrightarrow{a}$，根据三角形法则即可得$\overrightarrow{AC}$即为所求．
解答 
解：如图，$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{b}$，$\overrightarrow{BC}$=2$\overrightarrow{a}$，
则$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=2$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$．
则$\overrightarrow{AC}$即为所求．
点评 此题考查了平面向量的知识．注意三角形法则的应用．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
10．下列式子化简不正确的是（ ）
| A． | +（-5）=-5 | B． | -（-0.5）=0.5 | C． | -|+3|=-3 | D． | -（+1$\frac{1}{2}$）=1$\frac{1}{2}$ |
如图，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点P，则k的值为-6．
11．
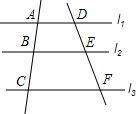如图，l1∥l2∥l3，则下列等式错误的是（ ）
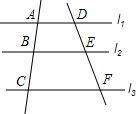如图，l1∥l2∥l3，则下列等式错误的是（ ）| A． | $\frac{BC}{AC}=\frac{EF}{DF}$ | B． | $\frac{AB}{AC}=\frac{DE}{DF}$ | C． | $\frac{AB}{DE}=\frac{BC}{EF}$ | D． | $\frac{AB}{AC}=\frac{AD}{CF}$ |
