题目内容
18.已知a为不等于2,b为不等于-1的有理数,则$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$的值不可能是( )| A. | 2 | B. | -2 | C. | 1 | D. | 0 |
分析 根据题意分别利用当a-2>0,b+1>0时,当a-2>0,b+1<0时,当a-2<0,b+1>0时,当a-2<0,b+1<0时,得出答案即可.
解答 解:∵a为不等于2,b为不等于-1的有理数,
∴当a-2>0,b+1>0时,
∴$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$=2,
当a-2>0,b+1<0时,
∴$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$=0,
当a-2<0,b+1>0时,
∴$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$=0,
当a-2<0,b+1<0时,
∴$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$=-2,
故$\frac{{|{a-2}|}}{a-2}+\frac{{|{b+1}|}}{b+1}$的值不可能是1.
故选:C.
点评 此题主要考查了代数式求值,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
10.如图,数轴上A,B两点分别对应有理数a,b,则a,-a,b,-b,1比较大小正确的是( )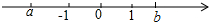
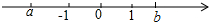
| A. | a<-a<b<-b<1 | B. | a<-b<b<1<-a | C. | a<b<-a<-b<1 | D. | a<-b<1<b<-a |
7.抛物线y=5x2先向上平移2个单位,再向右平移3个单位,所得的抛物线的解析式是( )
| A. | y=5(x+3)2+2 | B. | y=5(x-3)2+2 | C. | y=5(x+3)2-2 | D. | y=5(x-3)2-2 |


 如图,在正方形ABCD中AB=AD,∠B=∠D=90°.
如图,在正方形ABCD中AB=AD,∠B=∠D=90°.