题目内容
 如图,AD是△CAB的角平分线,∠B=34°,∠DAC=30°,则∠ACB的度数是( )
如图,AD是△CAB的角平分线,∠B=34°,∠DAC=30°,则∠ACB的度数是( )| A、96° | B、86° |
| C、76° | D、60° |
考点:三角形内角和定理
专题:
分析:根据角平分线的定义可得∠BAC=2∠DAC,再利用三角形的内角和等于180°列式计算即可得解.
解答:解:∵AD是△CAB的角平分线,
∴∠BAC=2∠DAC=2×30°=60°,
在△ABC中,∠ACB=180°-∠BAC-∠B=180°-60°-34°=86°.
故选B.
∴∠BAC=2∠DAC=2×30°=60°,
在△ABC中,∠ACB=180°-∠BAC-∠B=180°-60°-34°=86°.
故选B.
点评:本题考查了三角形的内角和定理,角平分线的定义,是基础题,熟记定理并准确识图理清角度之间的关系是解题的关键.

练习册系列答案
相关题目
下列命题中,真命题的个数为( )
①三角形两角的平分线交点到三角形三个顶点的距离相等
②三角形两边的中垂线的交点到三角形三边的距离相等
③等腰三角形底边中线上的一点到两腰的距离相等
④等腰三角形顶角的平分线与一腰的中垂线的交点到三角形三个顶点的距离相等.
①三角形两角的平分线交点到三角形三个顶点的距离相等
②三角形两边的中垂线的交点到三角形三边的距离相等
③等腰三角形底边中线上的一点到两腰的距离相等
④等腰三角形顶角的平分线与一腰的中垂线的交点到三角形三个顶点的距离相等.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知α,β是锐角,sinα=
,cosβ=
,则α+β等于( )
| 1 |
| 2 |
| ||
| 2 |
| A、60° | B、75° |
| C、90° | D、120° |
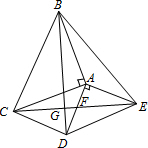 如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE,若AE=4,则CG的长为
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE,若AE=4,则CG的长为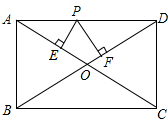 如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )
如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( ) 如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=52°,则∠BEC=
如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=52°,则∠BEC=