题目内容
13.先化简,再求值:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷(x-2-$\frac{12}{x+2}$)-$\frac{1}{x+4}$,其中x=2cos45°-$\sqrt{3}$tan60°+tan45°.
分析 先把分子分母因式分解,再把括号里面的通分,最后把x的值代入计算即可.
解答 解:∵x=2cos45°-$\sqrt{3}$tan60°+tan45°=2×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$×$\sqrt{3}$+1
=$\sqrt{2}$-2;
∴原式=$\frac{(x-4)^{2}}{x(x+2)}$÷$\frac{{x}^{2}-4-12}{x+2}$-$\frac{1}{x+4}$
=$\frac{x-4}{x(x+4)}$-$\frac{1}{x+4}$
=$\frac{x-4-x}{x(x+4)}$
=-$\frac{4}{x(x+4)}$,
当x=$\sqrt{2}$-2时,原式=-$\frac{4}{(\sqrt{2}-2)(\sqrt{2}+2)}$=2.
点评 本题考查了分式的化简求值,掌握分式的约分、通分以及特殊角的三角函数值是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
5.用配方法解一元二次方程x2+4x-3=0时,原方程可变形为( )
| A. | (x+2)2=1 | B. | (x+2)2=19 | C. | (x+2)2=13 | D. | (x+2)2=7 |
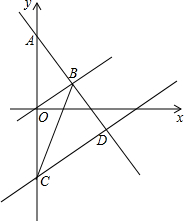 如图,在平面直角坐标系中,一次函数y=-x+b的图象与正比例函数y=kx的图象都经过点B(3,1)
如图,在平面直角坐标系中,一次函数y=-x+b的图象与正比例函数y=kx的图象都经过点B(3,1)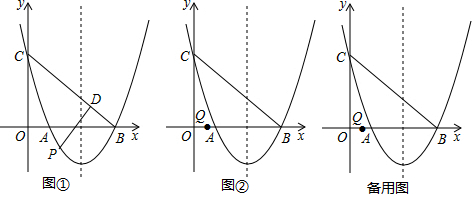
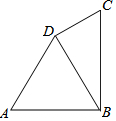 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠BDC=90°,BC=10cm,求△BCD的面积.
如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠BDC=90°,BC=10cm,求△BCD的面积.