Question

4．如图，在Rt△ABC中，∠ACB=90°，AB=8cm，AC=4cm，点D从点B出发，以每秒$\sqrt{3}$cm的速度在射线BC上匀速运动，当点D运动多少秒时，以A、D、B为顶点的三角形恰为等腰三角形？（结果可含根号）．

Answer 1

分析 分三种情况：①当 AB=AD 时，如图1，根据30°的三角函数列式计算即可；②当AB=BD时，如图2，则$\sqrt{3}$t=8，求出t；③当AD=AB时，如图3，根据BD=2BC列式，求t的值．

解答 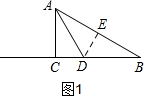解：在Rt△ABC中，
∵∠ACB=90°，AB=8 cm，AC=4 cm，
∴BC=$\sqrt{A{B^2}-A{C^2}}$=$4\sqrt{3}$cm
∵点D从点B出发，以每秒$\sqrt{3}$cm的速度在射线BC上匀速运动，
则BD=$\sqrt{3}$tcm，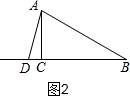
以A、D、B为顶点的三角形恰为等腰三角形时，分三种情况：
①当 AB=AD 时，如图1，过D作DE⊥AB于E，则AE=BE=$\frac{1}{2}$AB=4，
在Rt△ACB中，∵AC=4，AB=8，
∴∠B=30°，
cos∠B=cos30°=$\frac{BE}{BD}$，
∴$\frac{4}{\sqrt{3}t}=\frac{\sqrt{3}}{2}$，
t=$\frac{8}{3}$；
②当AB=BD时，如图2，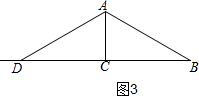
∵AB=8，BD=$\sqrt{3}$t，
则$\sqrt{3}$t=8，
t=$\frac{8\sqrt{3}}{3}$；
③当AD=AB时，如图3，
∵∠ACB=90°，
∴DC=BC=4$\sqrt{3}$，
则$\sqrt{3}$t=8$\sqrt{3}$，
t=8；
答：当点D运动8秒或$\frac{{8\sqrt{3}}}{3}$秒或$\frac{8}{3}$秒时，△ABD为等腰三角形．

点评 本题主要考查等腰三角形的性质和判定，由条件分三种情况分别得到关于t的方程是解题的关键，是常考题型；由动点组成的等腰三角形要采用分类讨论的思想．