Question

15．在正方形ABCD中，点E为BC边上一点且CE=2BE，点F为对角线BD上一点且BF=2DF，连接AE交BD于点G，过点F作FH⊥AE于点H，连结CH、CF，若HG=2cm，则△CHF的面积是$\frac{56}{5}$cm²．

Answer 1

分析 如图，过F作FI⊥BC于I，连接FE，FA，得到FI∥CD，设BE=EI=IC=a，CE=FI=2a，AB=3a，由勾股定理得到FE=FC=FA=$\sqrt{5}$a，推出HE=$\frac{1}{2}$AE=$\frac{\sqrt{10}a}{2}$，根据正方形的性得到BG平分∠ABC，由三角形角平分线定理得到$\frac{EG}{AG}=\frac{BE}{AB}$=$\frac{1}{3}$，求得HG=$\frac{1}{4}$AE=$\frac{\sqrt{10}}{4}$a=2，于是得到结论．

解答 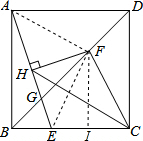解：如图，过F作FI⊥BC于I，连接FE，FA，
∴FI∥CD，
∵CE=2BE，BF=2DF，
∴设BE=EI=IC=a，CE=FI=2a，AB=3a，
∴则FE=FC=FA=$\sqrt{5}$a，
∴H为AE的中点，
∴HE=$\frac{1}{2}$AE=$\frac{\sqrt{10}a}{2}$，
∵四边形ABCD是正方形，
∴BG平分∠ABC，
∴$\frac{EG}{AG}=\frac{BE}{AB}$=$\frac{1}{3}$，
∴HG=$\frac{1}{4}$AE=$\frac{\sqrt{10}}{4}$a=2，
∴a=$\frac{4}{5}\sqrt{10}$，
∴S_△CHF=S_△HEF+S_△CEF-S_△CEH=$\frac{1}{2}$（$\frac{\sqrt{10}}{2}$a）²+$\frac{1}{2}$•2a•2a-$\frac{1}{2}$•2a•$\frac{3}{2}$a=$\frac{7}{4}$a²=$\frac{56}{5}$，
故答案为：$\frac{56}{5}$．

点评 本题考查了正方形的性质，等腰三角形的判定和性质，平行线分线段成比例定理，正确的作出辅助线是解题的关键．