题目内容
如图，在?ABCD中，对角线AC、BD相交于O，E是BC的中点，AE交BD于F，已知BD=12cm，求OF的长．考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：利用平行四边形的性质得出△ADF∽△EBF，进而得出BF、BO的长，进而得出答案．
解答：解：∵在?ABCD中，对角线AC、BD相交于O，
∴BO=DO，AD=BC，AD∥BC，
∴△ADF∽△EBF，
∴
=
∵E是BC的中点，
∴
=
=
，
∵BD=12cm，
∴BF=4cm，BO=6cm，
∴FO=2cm．
解：∵在?ABCD中，对角线AC、BD相交于O，∴BO=DO，AD=BC，AD∥BC，
∴△ADF∽△EBF，
∴
| BE |
| AD |
| BF |
| DF |
∵E是BC的中点，
∴
| BE |
| AD |
| BF |
| DF |
| 1 |
| 2 |
∵BD=12cm，
∴BF=4cm，BO=6cm，
∴FO=2cm．
点评：此题主要考查了平行四边形的性质以及相似三角形的判定性质，得出△ADF∽△EBF是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
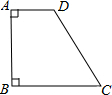如图，四边形ABCD中，∠A=∠B=90°，∠C=60°，CD=2AD．AB=4
如图，正方形ABCD内一点，PA=1，PD=2，PC=3，将△PDC绕着D点按逆时针旋转90°到△AQD的位置．