题目内容
已知方程x2+ax+b=0的两根均大于2,求a、b的关系式.
考点:根与系数的关系,根的判别式
专题:计算题
分析:设方程x2+ax+b=0的两根分别为m、n,根据根与系数的关系得到m+n=-a,mn=b,由题意得m-2>0,n-2>0,则(m-2)(n-2)>0,所以mn-2(m+n)+4>0,于是有b+2a+4>0,再根据根的判别式的意义得到△=a2-4b≥0,由此可得到a、b满足的关系式.
解答:解:设方程x2+ax+b=0的两根分别为m、n,则m+n=-a,mn=b,
∵m>2,n>2,即m-2>0,n-2>0,
∴(m-2)(n-2)>0,
即mn-2(m+n)+4>0,
∴b+2a+4>0,
而△=a2-4b≥0,
∴a、b的关系式为2a+b+4>0且a2-4b≥0.
∵m>2,n>2,即m-2>0,n-2>0,
∴(m-2)(n-2)>0,
即mn-2(m+n)+4>0,
∴b+2a+4>0,
而△=a2-4b≥0,
∴a、b的关系式为2a+b+4>0且a2-4b≥0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于O,E是BC的中点,AE交BD于F,已知BD=12cm,求OF的长.
如图,在?ABCD中,对角线AC、BD相交于O,E是BC的中点,AE交BD于F,已知BD=12cm,求OF的长.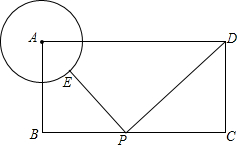 如图,矩形ABCD中,AB=2,BC=3,以A为圆心,1为半径画⊙A,E是圆⊙A上一动点,P是BC上一动点,则PE+PD最小值是( )
如图,矩形ABCD中,AB=2,BC=3,以A为圆心,1为半径画⊙A,E是圆⊙A上一动点,P是BC上一动点,则PE+PD最小值是( ) 正方形ABCD中,E是CB延长线上一点,G是AE上一点,且AG=AD,AF⊥AE,交GD于F,GD交AB于H,求证:AF+BE=AE.
正方形ABCD中,E是CB延长线上一点,G是AE上一点,且AG=AD,AF⊥AE,交GD于F,GD交AB于H,求证:AF+BE=AE.