题目内容
 如图,已知△ABC
如图,已知△ABC(1)画出△ABC关于y轴对称的△A1B1C1;
(2)直接写出:△A1B1C1的面积是
(3)在y轴上求作一点P,使PA+PC的值最小(不写画法、保留作图痕迹)
考点:作图-轴对称变换,轴对称-最短路线问题
专题:
分析:(1)根据关于y轴对称的特点画出△A1B1C1即可;
(2)根据△A1B1C1的面积=矩形的面积-三个三角形的面积即可得出结论;
(3)连接A1C交y轴于点P,则点P即为所求点.
(2)根据△A1B1C1的面积=矩形的面积-三个三角形的面积即可得出结论;
(3)连接A1C交y轴于点P,则点P即为所求点.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)△A1B1C1的面积=3×5-
×2×3-
×2×3-
×1×5
=15-3-3-
=
.
故答案为:
;
(3)连接A1C交y轴于点P,则点P即为所求点.
 解:(1)如图所示:
解:(1)如图所示:(2)△A1B1C1的面积=3×5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=15-3-3-
| 5 |
| 2 |
=
| 13 |
| 2 |
故答案为:
| 13 |
| 2 |
(3)连接A1C交y轴于点P,则点P即为所求点.
点评:本题考查的是作图-轴对称变换,熟知轴对称图形的作法及性质是解答此题的关键.

练习册系列答案
相关题目
对于(-2)4和-24,下列说法正确的是( )
| A、它们的意义相同 |
| B、它们的结果相同 |
| C、它们的意义不同,结果相同 |
| D、它们的意义不同,结果也不同 |
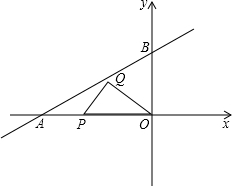 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
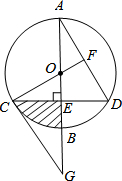 如图,已知⊙O的直径AB垂直弦CD于点E,过C点作⊙O的切线CG交AB延长线于点G,连接CO并延长交AD于点F,且AF=FD.
如图,已知⊙O的直径AB垂直弦CD于点E,过C点作⊙O的切线CG交AB延长线于点G,连接CO并延长交AD于点F,且AF=FD.
