题目内容
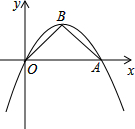 抛物线y=ax2+bx经过点A(4,0),B(2,2),连结OB,AB.
抛物线y=ax2+bx经过点A(4,0),B(2,2),连结OB,AB.(1)求a、b的值;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法代入二次函数解析式求出a,b的值即可;
(2)利用已知得出∠BOC=∠OBC=∠BAC=∠ABC=45°,即可得出∠OBA=90°,OB=AB,进而得出答案;
(3)利用已知得出点A'坐标,进而得出P点坐标,再利用抛物线解析式求出此点是否在抛物线上.
(2)利用已知得出∠BOC=∠OBC=∠BAC=∠ABC=45°,即可得出∠OBA=90°,OB=AB,进而得出答案;
(3)利用已知得出点A'坐标,进而得出P点坐标,再利用抛物线解析式求出此点是否在抛物线上.
解答: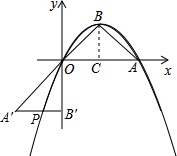 (1)解:由题意,得:
(1)解:由题意,得:
,
解得:
;
(2)证明:过点B作BC⊥x轴于点C,则OC=BC=AC=2,
∴∠BOC=∠OBC=∠BAC=∠ABC=45°,
∴∠OBA=90°,OB=AB,
∴△OAB是等腰直角三角形;
(3)解:∵△OAB是等腰直角三角形,OA=4,
∴OB=AB=2
,
由题意,得:点A'坐标为(-2
, -2
),
∴A'B'的中点P的坐标为(-
, -2
),
当x=-
时,y=-
×(-
)2+2×(-
)≠-2
,
∴点P不在抛物线上.
 (1)解:由题意,得:
(1)解:由题意,得:
|
解得:
|
(2)证明:过点B作BC⊥x轴于点C,则OC=BC=AC=2,
∴∠BOC=∠OBC=∠BAC=∠ABC=45°,
∴∠OBA=90°,OB=AB,
∴△OAB是等腰直角三角形;
(3)解:∵△OAB是等腰直角三角形,OA=4,
∴OB=AB=2
| 2 |
由题意,得:点A'坐标为(-2
| 2 |
| 2 |
∴A'B'的中点P的坐标为(-
| 2 |
| 2 |
当x=-
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴点P不在抛物线上.
点评:此题主要考查了待定系数法求二次函数解析式以及等腰直角三角形的判定和性质以及图象上点的坐标性质等知识,根据已知得出P点坐标是解题关键.

练习册系列答案
相关题目
已知A地的海拨高度为-50米,B地比A地高30米,则B地的海拔高度为( )米.
| A、-80 | B、30 |
| C、-20 | D、20 |

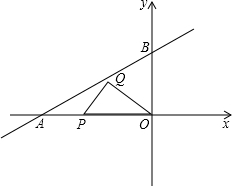 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB. 如图是钟表的表盘.
如图是钟表的表盘.