题目内容
9．若|a-1|+|b+3|+|2+c|=0，求a-b+c的值．分析 根据非负数的性质列方程求出a、b、c的值，然后代入代数式进行计算即可得解．
解答 解：根据绝对值非负性，可知：∵|a-1|≥0，|b+3|≥0，|2+c|≥0，
且|a-1|+|b+3|+|2+c|=0，
所以，|a-1|=0，|b+3|=0，|2+c|=0，
所以，a=1，b=-3，c=-2，
将a=1，b=-3，c=-2代入a-b+c，得a-b+c=1-（-3）+（-2）=2．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
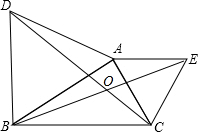△ABD和△AEC都是等边三角形，连CD、BE，若BE=6，求DC的长．
有理数a，b在数轴上的对应点如图所示，则下列式子中：①-b＞a；②|b|＜|a|；③a-b＞a+b；④|a|+|b|＞|a-b|，正确的有（ ）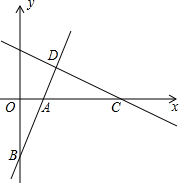
如图，直线y=2x+b经过点A（1，0），与y轴交于点B，直线y=ax+$\frac{8}{5}$经过点C（4，0），且与直线AB交于点D．