题目内容
14.已知a,b,c满足$\sqrt{a-3}$+|b-4|+c2-6c+9=0,求a+b-c的平方根.分析 根据非负数的在列方程求出a、b、c的值,然后代入代数式求值,再根据平方根的定义解答.
解答 解:$\sqrt{a-3}$+|b-4|+(c-3)2=0,
所以,a-3=0,b-4=0,c-3=0,
解得a=3,b=4,c=3,
所以,a+b-c=3+4-3=4,
所以,a+b-c的平方根是±2.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
2.下列说法正确的是( )
| A. | 绝对值等于本身的数是正数 | B. | -a是负数 | ||
| C. | 有理数不是正数就是负数 | D. | 分数都是有理数 |
19.我们知道:1+3=4,1+3+5=9,1+3+5+7=16,…,观察下面的一列数:-1,2,-3,4,-5,6,…将这些数排成如图的形式,根据其规律猜想:第20行第3个数是( )
| -1 | ||||||
| 2 | -3 | 4 | ||||
| -5 | 6 | -7 | 8 | -9 | ||
| 10 | -11 | 12 | -13 | 14 | -15 | 16 |
| … |
| A. | 363 | B. | 364 | C. | -363 | D. | -364 |
3.若一个正比例函数的图象经过不同象限的两点A(-2,m),B(n,3),那么一定有( )
| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n>0 | D. | m<0,n<0 |
 如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数为39°.
如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数为39°. 如图所示,已知线段m,n,求作线段AB,使它等于m+2n.(用尺规作图,不写做法,保留作图痕迹.)
如图所示,已知线段m,n,求作线段AB,使它等于m+2n.(用尺规作图,不写做法,保留作图痕迹.)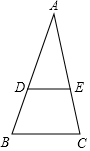 将下列求解过程的理由补充完整.如图,∠ADE=60°,∠B=60°,∠C=80°,求∠AED的度数.解:∵∠ADE=∠B=60°已知
将下列求解过程的理由补充完整.如图,∠ADE=60°,∠B=60°,∠C=80°,求∠AED的度数.解:∵∠ADE=∠B=60°已知