题目内容
18.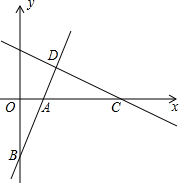 如图,直线y=2x+b经过点A(1,0),与y轴交于点B,直线y=ax+$\frac{8}{5}$经过点C(4,0),且与直线AB交于点D.
如图,直线y=2x+b经过点A(1,0),与y轴交于点B,直线y=ax+$\frac{8}{5}$经过点C(4,0),且与直线AB交于点D.(1)求B、D两点的坐标;
(2)求△ADC的面积;
(3)在直线BD上是否存在一点P,使S△ACP=2S△ACD?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
分析 (1)根据代入法进行解答即可;
(2)利用三角形的面积公式计算即可;
(3)利用三角形的面积公式计算解答.
解答 解:(1)将点A(1,0)代入y=2x+b中得b=-2,
即为y=2x-2,
∵DB相交于y轴,
∴令x=0,
∴y=-2,
∴B(0,-2),
将C(4,0)代入y=ax+$\frac{8}{5}$中得:a=-$\frac{2}{5}$,
即为y=$-\frac{2}{5}x+\frac{8}{5}$,
∵D相交于两线之间
∴$-\frac{2}{5}x+\frac{8}{5}=2x-2$,
∴x=$\frac{3}{2}$,
将x=$\frac{3}{2}$代入y=2x-2中得:y=1,
∴D(1.5,1),
(2)${S}_{△ADC}=AC×{y}_{D}×\frac{1}{2}=3×1×\frac{1}{2}=\frac{3}{2}$,
(3)假设存在P,
则S△ACP=2S△ACD=3,
∴${S}_{△ACP}=AC×{y}_{P}×\frac{1}{2}$,
∴yP=2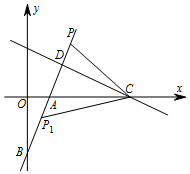
将yP=2代入y=2x-2中
∴x=2,
∴P(2,2),
${S}_{△ACP}=AC×|{y}_{{P}_{2}}|×\frac{1}{2}$
∴$|{y}_{{P}_{2}}|=2$,
∴${y}_{{P}_{2}}=-2$,
将y=-2代入y=2x-2中得
x=0,
∴P2(0,-2)
即D的坐标轴为(2,2)和(0,-2).
点评 本题考查了两直线的交点,要求利用图象求解各问题,要认真体会点的坐标.

练习册系列答案
相关题目
3.若一个正比例函数的图象经过不同象限的两点A(-2,m),B(n,3),那么一定有( )
| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n>0 | D. | m<0,n<0 |
7. 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )| A. | 25cm | B. | 50cm | C. | 75cm | D. | 100cm |
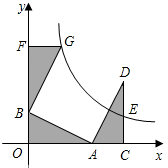 如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=$\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象过CD的中点E.
如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=$\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象过CD的中点E. 如图所示,已知线段m,n,求作线段AB,使它等于m+2n.(用尺规作图,不写做法,保留作图痕迹.)
如图所示,已知线段m,n,求作线段AB,使它等于m+2n.(用尺规作图,不写做法,保留作图痕迹.) 如图所示,为修铁路需凿通隧道AC,测得∠C=90°,AB=5km,BC=4km,若每天凿0.3km,试计算需要几天才能把隧道AC凿通?
如图所示,为修铁路需凿通隧道AC,测得∠C=90°,AB=5km,BC=4km,若每天凿0.3km,试计算需要几天才能把隧道AC凿通?