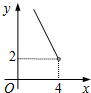题目内容
17. 如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题:
如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题:(1)a的值为2.5.
(2)不解关于x、y的方程组$\left\{\begin{array}{l}{y=0.5x+3}\\{y=mx+n}\end{array}\right.$,直接写出它的解为$\left\{\begin{array}{l}{x=-1}\\{y=2.5}\end{array}\right.$.
(3)若直线l1,l2表示的两个一次函数值都大于0,此时恰好-6<x<-$\frac{6}{11}$,求直线l2的函数解析式.
分析 (1)由点P在直线l1的图象上,代入即可求出a的值;
(2)由直线l1和l2的交点为点P,联立两函数解析式成方程组,方程组的解即为点P的坐标,由此即可得出结论;
(3)由x的取值范围即可得出点D的横坐标,由此即可得出点D的坐标,结合点P、D的坐标利用待定系数法即可求出直线l2的函数解析式.
解答 解:(1)∵点P(-1,a)在直线l1:y=0.5x+3的图象上,
∴a=0.5×(-1)+3=2.5.
故答案为:2.5.
(2)∵直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,2.5),
∴方程组$\left\{\begin{array}{l}{y=0.5x+3}\\{y=mx+n}\end{array}\right.$的解为:$\left\{\begin{array}{l}{x=-1}\\{y=2.5}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=-1}\\{y=2.5}\end{array}\right.$.
(3)由已知得:点D的坐标为(-$\frac{6}{11}$,0),
将点P(-1,2.5)、点D(-$\frac{6}{11}$,0)代入到y=mx+n中得:
$\left\{\begin{array}{l}{2.5=-m+n}\\{0=-\frac{6}{11}m+n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-5.5}\\{n=-3}\end{array}\right.$.
故直线l2的函数解析式为y=-5.5x-3.
点评 本题考查了一次函数与二元一次方程(组)以及待定系数法求函数解析式,解题的关键是:(1)将点P的坐标代入直线l1的解析式中;(2)由两直线的交点坐标即可得出方程组的解;(3)找出点D的坐标.本题属于基础题,难度不大,解决该题型题目时,由点的坐标利用待定系数法求出函数解析式是关键.

| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
| A. | 8x4y8 | B. | -8x4y8 | C. | 16xy8 | D. | 16x4y8 |
| A. | x3+x2=x5 | B. | x3-x2=x | C. | x3•x-2=x-5 | D. | x3÷x2=x |
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
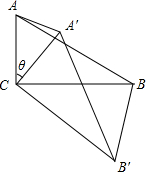 如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.
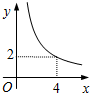
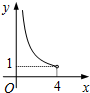
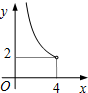
如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.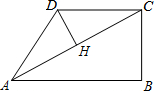 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )